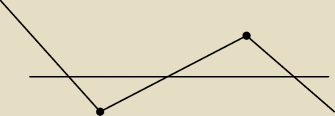
Esktrema lokalne funkcji - pochodna Michał: Wyznacz najmniejszą i największą wartość funkcji f w danym przedziale: f(x) = −1/3x³ − 1/2x² + 2x + 4 f'(x) = −x² − x + 2 x₁ = 1 X₂ = −2 f'(x) = −(x−1)(x+2) = 0 Maksimum jest w punkcie x₀ = 1, f(1) = 5¹₆ Nie mogę natomiast wyliczyć minimum, powinno być −2, ale wychodzą błędne wyniki.

Jerzy: Naszkicuj wykres pochodnej.

Jerzy: I jaki masz podany przedział ?

Michał: <−3; 3>

Jerzy: To teraz policz: f(1) f(−2) f(−3) f(3) i wybierz skrajne wartości.

Michał: Liczyłem i f(3) = −7/2 f(−3) = −9/2 f(1) = 5¹₆ f(−2) = 2/3 Maksimum w punkcie x₀ = 1 się zgadza. Minimum dla każdego z tych wyników nie zgadza się z odpowiedzią, bo powinno być minimum równe −3¹₃

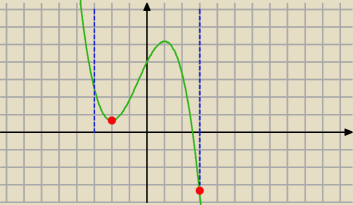
Jerzy: Musisz popełniać bład w obliczeniach.

Jerzy: Oczywiście f_max = f(1)

Jerzy:

	7		1
fmin = −		= −3
	2		2

Michał: Czyli to jest raczej błąd w książce? Bo z trzy razy podchodziłem do tego zadania i ciągle nie chciało mi wyjść to −3¹₃.

Jerzy: Masz dobry wynik , pomyłka w odpowiedzi.