zadanko zadanie: Wyznacz równania stycznych do okręgu x² + y² −2y −7=0 przechodzących przez punkt A = (4,5) Proszę o pomoc

zadanie: help

Jack: Znajdz srodek i promien okregu. Styczna do okregu jest oddalona od srodka okregu o promien. Skorzystaj ze wzoru na odleglosc prostej od punktu

zadanie: S = (0,−1) r = 2√2 Ale jak z tego wyznaczyc te prosta?

Jack: Prosta przechodzi przez punkt A zatem spelnia rownanie y=ax+b 5 = 4a+b no a stad b = 5−4a Zatem.mamy prosta y= ax + 5−4a Zapiszmy ja w postaci ogolnej ax − y + 5 − 4a = 0 Ze wzoru na odleflosc punktu od prostej : Nasz punkt S(0,−1) nasza odleglosc d=2√2 Prosta ax − y + 5 − 4a = 0 W czym problem?

Jack: Natomiast samo rownanie zle przeksztalcone (albo zle odczytane). x² + (y−1)² = 8 Zatem.S(0,1) r = √8 = 2√2

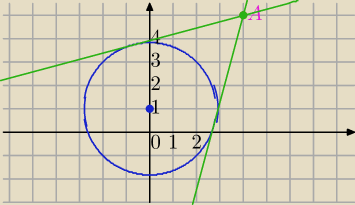
Mila: A(4,5) x² + y² −2y −7=0 x²+(y−1)²=8 S=(0,1), r=√8 k: y−5=m*(x−4) styczna do okręgu⇔mx−y−4m+5=0

	|m*0−1−4m+5|
d(S,k)=		=√8
	√m2+1

|−4m+4|=√8*(m²+1) /² 16m²−32m+16=8*(m²+1) 2m²−4m+2=m²+1 m²−4m+1=0 Δ=12 m=2−√3 lub m=2+√3 styczne: k₁: y=(2+√3)*(x−4)+5 k₂: y=(2−√3)*(x−4)+5

Antonni: Sposob nr 3 . Wyznaczamy punkty stycznosci 1. Liczymy dlugosc odcinka SA 2. Wyznaczamy wspolrzedne P srodka odcinka SA

	1
3.Piszemy rownanie pkregu o promieniu		SA i srodku o wspolrzednych P
	2

4.Liczymy wsporzedne punktow przeciecia sie tych dwoch okregow Dostalismy dwa punkty stycznosci. Piszsemy rownania prostych stycznych .

zadanie: Dzięki, a jakoś łatwo mozna odczytac kat miedzy nimi?

Adamm: https://matematykaszkolna.pl/strona/1228.html

Adamm: kąt to 60^o

Antonni: Wiesz ze prosta SA jest dwusieczna tego kąta Jesli sobie oznaczysz punty stycznosci przez np Q₁ i Q₂ to wiemy ze trojkat SQ₁A jest prostokatny wiec wyliczysz sobie kąt SAQ₁ Pomnozysz przez 2 i masz kąt miedzy stycznymi .