,., Pełcio: Dzień dobry Każdą podpowiedź się ceni: 1. Wyznacz najmniejszą wartość funkcji f(x)= x(x+1)(x+2)(x+3) oraz argumenty, dla których funkcja ją osiąga. 2. Wyznacz liczbę pierwiastków rzeczywistych równania x*|x|= x+k w zależności od parametru k. k= x*(|x|−1), ale jak wyznaczać tą liczbę w zależności od k? 3. Rozwiąż równanie z niewiadomą x, jeśli |a|≥2.

	a+1
(1+x+x2)2=		(1+x2+x4)
	a−1

doszedłem do czegoś takiego:

	1
x(x2+x+1)= (1+x2+x4)*
	a−1

i teraz:

	(x2+1)2−x2
a−1=
	x(x2+x+1)

	(x2+x+1)(x2−x+1)
a−1=
	x(x2+x+1)

	x2−x+1
a−1=
	x

	1
a= x−1+		+1
	x

	1
a= x+
	x

Skoro |a|≥2 ⇒ x∊ℚ\{0}, tutaj proszę o weryfikację, nie jestem pewny 4. Od trójkąta o danych długościach boków 7,8,9 odcięto trzy trójkąty narożne prostymi równoległymi do boków tego trójkąta i stycznymi do koła wpisanego w ten trójkąt. Oblicz sumę pól wpisanych w trójkąty narożne. 5. Wykaż, że jeżeli wielomian ax³+bx²+cx+d ma dwa pierwiastki będące liczbami przeciwnymi, to ad=bc. Tutaj proszę o sprawdzenie czy tak może być. Teza: ad−bc=0 Zapisujemy nasz wielomian w postaci: W(x)= a(x−p)(x+p)(x+q) W(x)= ax³+azx²−ap²x−azp² i teraz: a*(−azp²)− az*(−ap²)= −a²p²z+a²p²z=0 c.n.d. 6. Wyznacz a i b tak, aby były one równocześnie pierwiastkami dwukrotnymi wielomianu: W(x)= x⁴+2ax³+3(b+1)x²−4x+4 Też proszę o sprawdzenie. Zapisujemy nasz wielomian w postaci: W(x)= (x−p)²(x−q)² W(x)= (x²−2xp+p²)(x²−2xq+q²)= x⁴−(2q+2p)x³+(q²+4pq+p²)x²−(2pq²+2p²q)x+p²q² więc: 2a= −2q−2p i 3b+3= q²+4pq+p² i −2pq²−2p²q=−4 i p²q²= 4

	q2+4pq+p2
a= −q−p b=		−1 pq(q+p)=2 pq=2 lub pq=−2
	3

z ostatniego warunku mamy 1) pq=2, wtedy p+q= 1 a= −1

	1+4		2
b=		−1=
	3		3

2) pq=−2, wtedy p+q=−1 a= 1

	1−4
b=		−1= −2
	3

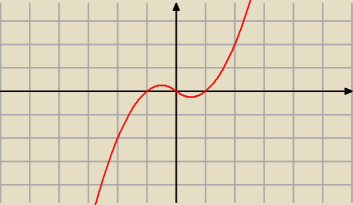
Adamm: 4. popraw treść (pola wpisane?) 2. bardzo łatwo graficznie dla x∊(−∞;−1/4)∪(1/4;∞) jedno rozwiązanie dla x∊{−1/4;1/4} dwa rozwiązania dla x∊(−1/4;1/4) trzy rozwiązania

Pełcio: 4. tam ma być oczywiście suma pól kół wpisanych w te narożne trójkąty 2. rzeczywiście, źle to rysowałem

Adamm: 1. t=x+1,5 f(t)=(t−1,5)(t−0,5)(t+0,5)(t+1,5)=(t²−2,25)(t²−0,25)=t⁴−2,5t²+0,5625= =(t²−1,25)²−1≥−1 i osiąga tą wartość dla t=±√5/2 czyli x=±√5/2+3/2

Adamm: oczywiście dla x=±√5/2−3/2

Pełcio: Dziękuję. A te co ja napisałem są ok?

Pełcio: Może ktoś popatrzeć na te zadanka, czy są dobrze zrobione?