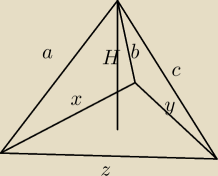Prosze o pomoc
ja: Rozpatrzmy w przestrzeni trzy wzajemnie prostopadłe odcinki SA, SB, SC, które mają odpowiednio
długości a, b, c. Ile wynosi odległość punktu S od płaszczyzny ABC?
9 mar 14:14
Pytający: Oznaczmy: S=(0,0,0), A=(a,0,0), B=(0,b,0), C=(0,0,c). Wtedy równanie odcinkowe płaszczyzny ABC
to:
Równanie ogólne:
| 1 | | 1 | | 1 | | 1 | | 1 | | 1 | |
| x+ |
| y+ |
| z−1=0 // współczynniki: A= |
| , B= |
| , C= |
| , D=−1 |
| a | | b | | c | | a | | b | | c | |
Odległość punktu S od płaszczyzny ABC wynosi:
| | | | 1 | | 1 | | 1 | | | |
| *0+ |
| *0+ |
| *0+(−1)| | | | a | | b | | c | |
| |
d= |
| = |
| | √(1/a)2+(1/b)2+(1/c)2 | |
| | √a2b2c2 | |
= |
| |
| | √a2b2+a2c2+b2c2 | |
9 mar 14:45
Adamm: ja jestem ciekaw dowodu geometrycznego

9 mar 15:13
Adamm: teraz niech x=
√a2+b2, y=
√b2+c2, z=
√a2+c2
| | 1 | | 1 | |
V= |
| * |
| *([x+y+z][x+y−z][x−y+z][−x+y+z])1/2*h |
| | 3 | | 4 | |
| | 2abc | |
stąd h= |
| |
| | ([x+y+z][x+y−z][x−y+z][−x+y+z])1/2 | |
teraz można wyliczyć [x+y+z][x+y−z][x−y+z][−x+y+z]

9 mar 15:34
Adamm:
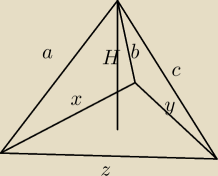
9 mar 15:35