parametr kama:

	1		1
Zbadaj liczbę rozwiązań równania −		x2−		|x| +3 =m w zależności od parametru m.
	2		2

dwa przypadki rozpatryję dla x≥0 i x<0

	1		1
1. dla x≥0 −		x2−		x +3
	2		2

wyszły mi miejsca zerowe 2 i −3 ramiona w dół i mam problem myślę zwykły wyliczeniowy z q=²⁵₈ i w tym momencie wiem że już mi nie wyjdzie kurcze co źle potem wiem

	1		1
2.dla x<0 −		x2+		(x) +3 wykres i prosta patrzeć jak się przesuwa ale wiem że to
	2		2

nieszczęsne q jest już źle pewnie czegoś nie dostrzegłam

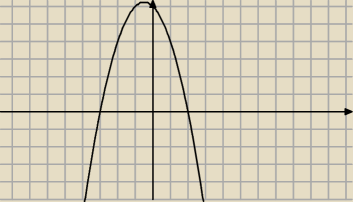
Jerzy: W pierwszym masz dobrze : q = U{25}[8}

kama: kurcze to chyba jednak tego nie rozumiem trzy przykłady wyszły a w tym problem. W drugim wierzchołek ten sam miejsca zerowe 3 i −2 jak narysowałam podobnie jak u Ciebie to kompletnie nic nie wychodzi przecież miejsce przecięcia z osią Y jest 3, a ten wierzchołek to więcej niż 3 w odpowiedzi tego w ogóle nie uwzględnili stąd stanęłam na tym q

kama:

	25
w odpowiedzi jest:brak dla (3,∞) no skąd według mnie tu już powinno być brak dla (		,∞)
	8

	25		1
przecież		=3
	8		8

Jerzy: Bo żle interpretujesz ... naszkicuj wykres całej funkcji.

Jerzy: Przecież po narysowaniu , wierzchołki zostaną "odciete" od wykresu i najwyższym punktem całego wykresu będzie punkt (0,3)

kama: wierzchołki mam obliczone obie parabole ramiona w dół miejsca zerowe są i potem jadę prostą równoległa do osi X przecież jak dojadę tą prostą do wierzcołka czyli owe 3{1}{8} to dalej nie mamm już żadnego wykresu. więc powinno być brak rozwiązania podpowiedz co źle myślę ?

Jerzy: Czytaj wyżej ... rysujesz oddzielnie dla x ≥ 0 i x < 0 , te dwie "połowki" wykresu zbiegną sie w punkcie (0,3) ... tych wierzchołków już nie będzie na wykresie.

kama: wiem o tym zbiegnięciu tylko nie wiem czemu ja nadal rysuję i co gorsza widzę wierzchołki /całkiem ładne takie coś jakby serce

Jerzy: Teraz jasne ?

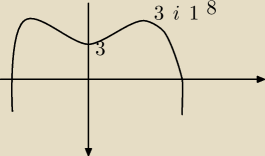
kama: Niestety nie, widzę wierzchołki , niestety tak to widzę

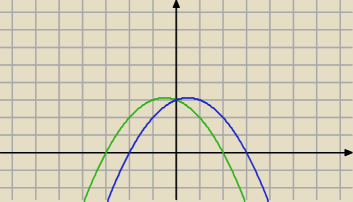
Jerzy: No to żle widzisz.... Teraz niebieską wymazujesz dla : x ≥ 0 , a zieloną wymazujesz dla: x <0 Pozostaje wykres całej funkcji, który ma wierzchołek w punkcie: (0,3)

kama: żesz powaliło mi się z igrekami. Dziękuję

kama: Hehe idę do okulisty.