Równanie stycznej do wykresu funkcji - pochodna
Michał: | | 1 − 6x2 | |
Wyznacz równanie stycznej do wykresu funkcji f(x) = |
| : przechodzącej przez |
| | 6x2 | |
punkt P(−3;
12).
| | −1 | |
Pochodna to f'(x) = |
| |
| | 3x3 | |
Liczę z wzoru y = f'(x
0) * (x − x
0) + f(x
0)
| | 1 | | 1 | |
I wychodzi y = |
| * (x + 3) + |
| |
| | 81 | | 2 | |
Proszę o pomoc.
9 mar 09:24
Jerzy:
Punkt P nie jest punktem styczności.
9 mar 09:27
Michał: Czyli tylko funkcja do której styczną mam wyznaczyć, przechodzi przez ten punkt? W takim razie
co z tym dalej zrobić?
9 mar 09:31
Jerzy:
Nie rozumiesz ... prosta ma być styczna do wykresu funkcji i przechodzić przez punkt P,
który nie należy do krzywej ( czyli: x0 = −3 jes błędnym założeniem)
9 mar 09:35
Janek191:
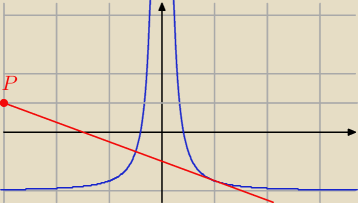
9 mar 09:38
Jerzy:
Z warunku,że styczna przechodzi przez P , wyznacz: x0
9 mar 09:42
Michał: y = ax + b
1/2 = −3a + b
I zamiast a, b mam podstawić kolejno f'(x0) i b = f(x0) − f'(x0) * x0?
9 mar 09:57
Jerzy:
Styczna z 9:24 ma przechodzić przez punkt P.
9 mar 10:02
Michał: 9x03 − 7x0 − 18 = 0
9 mar 10:20
Jerzy:
Patrząc na rysunek: x0 = 1
9 mar 10:23
Jerzy:
(Zakładając,że rysunek jest dobry )
9 mar 10:24
Michał: Ładnie wychodzi, dziękuję. Tylko jeszcze chciałbym się zapytać czy dobrze liczyłem x0 i po
prostu się pomyliłem w obliczeniach czy po prostu to był zły sposób:
y − f(x0) = f'(x0)(x − x0)
12 − (1 − 6x2) / (6x2) = (−1 / x3) * (−3 − x); x0 jako x
9 mar 10:29
Jerzy:
Dobrze .... to Ci sugerowałem 10:02
9 mar 10:33
Michał: Wiem, ale od ponad roku nie robiłem zadań z pochodnych i nie wiedziałem o co chodzi na
początku. Jeszcze raz dziękuję.
9 mar 10:35
adam:
Równanie stycznej: y = −x/3 − 1/2
Punkt styczności: (1, −5/6)
9 mar 18:23
