Wyznacz dziedzinę naturalną and: Wyznacz dziedzinę naturalną, zbiór miejsc zerowych oraz wszystkie asymptoty funkcji f(x) = ln(10−x²) Z góry dziękuję

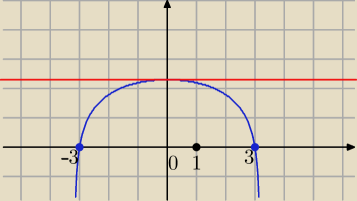
Janek191: Dziedzina naturalna: 10 − x² > 0 ⇔ ( √10 − x)*(√10 + x) > 0, więc x ∊ ( − √10 , √10 )

Janek191: Miejsca zerowe: ln ( 10 − x²) = 0 ⇔ 10 − x² = 1 ⇔ x² = 9 ⇔ x = − 3 lub x = 3

Jerzy: Dziedzina: 10 − x² > 0 ⇔ (√10 + x)(√10 − x) > 0 ⇔ x ∊ (−√10;√10) lim_x→−√10 ln(10−x²) = −∞ lim_x→−√10 ln(10−x²) = −∞ Dwie asymptoty pionowe: x = −√10 oraz x = √10

Jerzy: Miejsca zerowe: ln (10 − x²) = 0 ⇔ 10 − x² = 1 ⇔ x² = 9 ⇔ x = 3 lub x = −3

Janek191:

	−2 x
f '(x) =		= 0 ⇔ x = 0
	10 − x2

	−2*(10 − x2) − (−2x)*( −2 x)		− 20 − 2 x2
f '' (x) =		=		< 0
	(10 − x2)2		(10 − x2)2

dla x ∊ Df zatem funkcja f osiąga maksimum lokalne y_max = f(0) = ln 10 Asymptota pozioma y = ln 10 ========== Patrz też na wykres funkcji f

Jerzy: Witaj Janek191 Funkcja nie posiada asymptoty poziomej, z to ma dwie pionowe.

Janek191: Maksimum lokalne jest równocześnie maksimum funkcji.

Janek191: Faktycznie − jeszcze śpię Pozdrawiam.

and: Dziękuję uprzejmie Panowie, teraz jest wszystko jasne