Znaleźć miejsce geometryczne punktów, z których można poprowadzić do elipsy NiceToMeetYou: Znaleźć miejsce geometryczne punktów, z których można poprowadzić do elipsy (x²)/(a²) + (y²)/(b²) = 1 dwie styczne prostopadłe. Hej! Bardzo proszę o pomoc w zadaniu. Wiem że wynik powinien być x² + y² = a² + b², że powinienem skorzystać z warunku na prostopadłość prostych i punktów (a,b), (−a,b), (−a,−b) i (a,−b), ale jakoś nie umiem tego złożyć w całość. Nie proszę o pełne rozwiązanie, ale chociaż o jakieś wskazówki, równanie, schemat, jak powinienem to zrobić

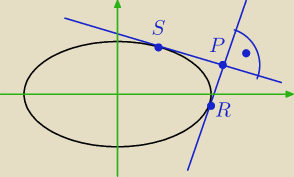
g: oznaczenia P=(x,y), S=(xs,ys), R=(xr,yr) warunek prostopadłości PS * PR = 0 (iloczyn skalarny) (x−xs)*(x−xr) + (y−ys)*(y−yr) = 0 x²+y² + xs*xr+ys*yr = x*(xs+xr)+y*(ys+yr) zapis parametryczny elipsy x = a cos t dx = −a sin t dt = −(a/b) y dt y = b sin t dy = b cos t dt = (b/a) x dt warunki styczności PS z elipsą 1) (xs/a)² + (ys/b)² = 1 2) PS x [dxs,dys] = 0 (iloczyn wektorowy) [x−xs,y−ys] x [−(a/b)ys, (b/a)xs] = 0 (x−xs)(b/a)xs + (y−ys)(a/b)ys = 0 / :ab x*xs/a² + y*ys/b² − 1 = 0 Z warunków styczności, zakładając dane x,y, wyznacz xs,ys,xr,yr i wstaw do równania z warunku prostopadłości.