wyznacz ekstrema funkcji papryk: f(x)=x*ln(x²) wyznacz ekstrema funkcji

papryk: wychodzi mi pochodna f'(x)=lnx² + ¹_x wychodzi na to, że funkcja jest rosnąca w całej dziedzinie? bo na moje oko ta pochodna nie ma miejsca zerowego

jo: Oblicz jeszcze raz pochodną...

papryk: f'(x)=ln(x²) + x* ¹_x² a jak inaczej?

jo: jeszcze musisz pomnożyć przez pochodną funkcji wewnętrznej:

	1
f'(x) = ln(x2) + x *		* 2x = ln(x2)+2
	x2

Bogdan: stosuj dużą literkę U przy zapisywaniu ułamków, kiepsko widać teraz ułamki

jo: Teraz wyznacz f'(x)=0, f'(x)<0, f'(x)>0

papryk: aaa bo jeszcze tam było złożenie funkcji, a ja je przeoczyłem to wychodzi na to, że wykres otrzymanej pochodnej ln(x²)+2 ma wartość zero wtedy, gdy ln(x²)=−2 dalej 10⁻² =x²

	1
więc x=		?
	10

dzięki za radę z tym dużym U

papryk:

	1
x>		to funkcja jest rosnąca
	10

	1
x<		funkcja jest malejąca, bo wykres pochodnej jest ujemny
	10

	1
zatem w punkcie x=		funkcja ma minimum?
	10

jo: ln(x²) −2 ⇒ e⁻² = x² ... pomyliło Ci się z log Spróbuj teraz dokończyć.

jo: oczywiście na początku ma być ln(x²) = −2

papryk: to będzie wtedy:

	1
x =		minimum tej funkcji
	e

jo: tak

papryk: uff dziękuję bardzo gratuluję pedagogicznego podejścia

jo: i max w tym drugim punkcie...

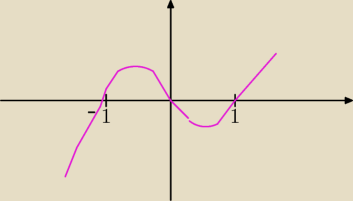
jo: Prawie tak ta funkcja będzie wyglądała

papryk: przy czym x nie należy do dziedziny