Wykaż, że długość odcinka AD wynosi u{24}{7} p{2} Olkowy: Kat BAC w trójkącie ABC jest prostokątny. Przyprostokątne mają długości 6 i 8. Dwusieczna kąta BAC przechodzi przez punkt D leżący na boku BC. Wykaż, że długość odcinka AD wynosi ²⁴₇√2

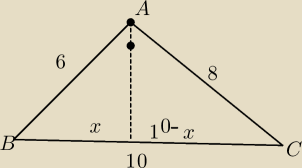
Antonni: Zastosuj tw o dwusiecznej kąta wewnetrznego trojkata \Potem policz dlugosc tej dwusiecznej

Olkowy: Mam x. Jak teraz policzyc długość dwusiecznej

Eta:

	1
P(ABC)=		*6*8= 24
	2

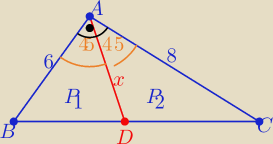
	1		6x√2		1		8x√2
P1=		*6*x*sin45o=		, P2=		*8*x*sin45o=
	2		4		2		4

P=P₁+P₂

	24√2
to 6x√2+8x√2=4*24 ⇒ 14x√2=4*24 ⇒ x=|AD|=.................=
	7