dowody geometryczne also: W trapezie ABCD o podstawach AB iCD przekatne przecinaja sie w punkcie E. Wykaz, ze pole trojkata AED jest srednia geometryczna pol trojkatow AEB i CED

Adamm:

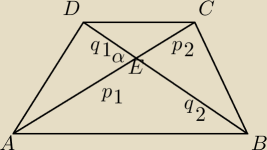
	1		1
PAEBPDEC=		p1*q2*p2*q1*sin2(180−α)=		p1*q2*p2*q1*sin2α
	4		4

ponieważ AEB oraz DEC są podobne to zachodzi p₂*q₂=p₁*q₁

	1		1
PAEBPDEC=		p1*q2*p2*q1*sin2α=(		p1q1sinα)2=PAED2
	4		2

P_AED=√P_AEBP_DEC c. b. d. o.

Adamm: polecam najpierw założyć że coś jest prawdziwe i wyciągnąć z tego wnioski, tak doszedłem do tego rozwiązania

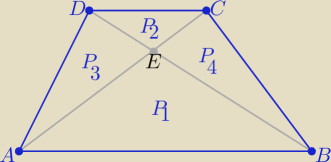
Eta: P₃=P₄ i z podobieństwa trójkątów ABE i DEC ( kkk) w skali k>0

	P1		√P1*P2
P3=P4=k*P2 i		=k2 ⇒		=k ⇒ P2*k=√P1*P2
	P2		P2

P₃=P₄=√P₁*P₂ c.n.w