Trójkąt prostokątny. Na przeciwprostokątnej wybrano punkt. Wiciu: Dany jest trójkąt prostokątny o przyprostokątnych długości: |BC | = 3 i |AC | = 4 . Na boku AB tego trójkąta wybrano taki punkt D , że ∘ |∡ACD | = 60 . Oblicz długość odcinka CD .

Eta:

	1
P(ABC)=		*4*3=6
	2

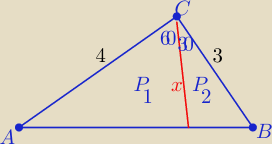
	1		1		3
P1=		*4*x*sin60o = x√3 , P2=		*3*x*sin30o =		x
	2		2		4

	3
to x√3+		x=6 /*4
	4

x(4√3+3)= 24 /*(4√3−3) x=.................................

	8(4√3−3)
Odp: x=
	13