Dla jakich wartości parametru m równanie (m+2)x^2-4mx+4m-1=0 ma dwa pierwiastk Mateusz: mam ciężkie zadanie nad których siedzę juz godzine . prosze o pomoc Dla jakich wartości parametru m równanie (m+2)x²−4mx+4m−1=0 ma dwa pierwiastki dodatnie?

Tadeusz: m+2≠0 Δ>0 x₁+x₂>0 x₁*x₂>0

'Leszek: Warunki rozwiazania zadania 1) Δ >0 2) x₁ + x₂ >0 3) x₁ *x₂ >0 4) m+2 ≠0 Do warunkow 2) i 3) wykorzystaj wzory Vietea

Janek191: 1) Δ > 0 2) x₁ + x₂ > 0 i x₁*x₂ > 0 wzory Viete'a 3) m ≠ − 2

yht: (m+2)x²−4mx+4m−1=0 a=(m+2), b=(−4m), c=(4m−1)

	−b
x1+x2 =
	a

	c
x1*x2 =
	a

Warunki: 1⁰: Δ>0 2⁰: x₁+x₂>0 3⁰: x₁*x₂>0 1⁰: Δ>0 b²−4ac>0 (−4m)²−4*(m+2)(4m−1)>0 16m²−4(4m²−m+8m−2)>0 16m²−16m²+4m−32m+8>0 −28m+8>0 −28m>−8 |:(−28)

	8
m<
	28

	2
m<
	7

	2
m∊(−∞,		)
	7

2⁰: x₁+x₂>0

−b
	> 0
a

4m
	>0
m+2

4m(m+2)>0 4m=0 ∨ m+2=0 m=0 ∨ m=−2 m∊(−∞,−2) ∪ (0,+∞) 3⁰: x₁*x₂>0

c
	> 0
a

4m−1
	>0
m+2

(4m−1)(m+2)>0 4m−1=0 ∨ m+2=0

	1
m=		∨ m=−2
	4

	1
m∊(−∞,−2) ∪ (		,+∞)
	4

część wspólna 1⁰, 2⁰, 3⁰:

	2		1
m∊(−∞,−2) ∪ (		,		)
	7		4

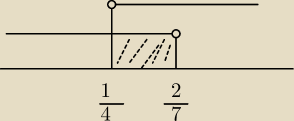
Mateusz: liczyłem tak jak piszecie ale dziwna suma rozwiązań wychodzi. do tej osi jeszcze powinien byc wynik m>0. zawsze wychodzily po 4 liczby teraz wyszly 3 i nie wiem jak to opisac na osi

Mateusz: dzieki yht!

yht: na końcu mam błąd

	1		2
powinno być m∊(−∞,−2) ∪ (		,		)
	4		7

	1		2
bo przecież		<
	4		7