Oblicz przekątną czworokąta Bułka: Treść zadania: Dany jest czworokąt o obwodzie 17 (p). Jedna z przekątnych dzieli go na dwa trójkąty, których obwody wynoszą 14 (p₁) i 15 (p₂). Oblicz długość tej przekątnej.

	1
W odpowiedziach jest		(p1+p2−p) = 6
	2

Czy ktoś wie dlaczego właśnie takie działanie?

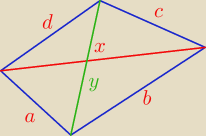
Janek191: Mamy a + b + c + d = 17 a + b + x = 15 c + d + x = 14 więc a + b + c + d + 2 x = 29 17 + 2 x = 29 2 x = 12 x = 6 =======

'Leszek: Niech a ,b ,c ,d boki czworokata , x przekatna czworokata Zatem obwod jednego Δ wynosi a + b +x = p₁ Obwod drugiego Δ wynosi c + d + x = p₂ Rownania dodajemy do siebie a+b+c +d +2x = p₁ + p ₂ oraz a + b +c+d = p Czyli

	p1 +p2 − p
x =
	2

Bułka: Dziękuję bardzo za wyjasnienia

Mateusz: rysujesz czworokąt . opisując kolejno boki a,b,c,d i przekątna e. trojkat a+d+e=14 2trojkat b+c+e=15 powstaje uklad równań , następnie sumujesz wszystko i powstaje a+b+c+d+2e=29 a+b+c+d=17 więc 17+2e=29 /−17 2e=12 e=6