Pomoże ktoś?? Nie mam pojęcia od czego się zabrać.. damian: Wyznacz wysokość prostopadłościanu wpisanego w kulę o promieniu R, wiedząc, że jego objętość jest największa z możliwych, a stosunek długości krawędzi podstawy wynosi 1:k.

damian: ktoś cos?

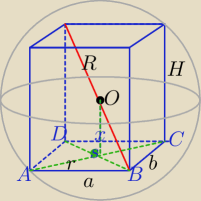
Mila: Prostopadłościan jest wpisany w kulę, gdy wszystkie jego wierzchołki leżą na powierzchni kuli.

b		1
	=
a		k

a=k*b |BD|²=a²+b²⇔|BD|²=k²b²+b² |BD|²=b²*(k²+1) (2R)²=H²+|BD|² 4R²=H²+b²*(k²+1)

	4R2−H2
b2=
	k2+1

V=a*b*H=k*b²*H

	k
V(H)=		*(4R2−H2)*H
	k2+1

	k
V(H)=		*(4R2*H−H3)
	k2+1

	k
V'(H)=		*(4R2−3H2)
	k2+1

Dokończ

damian: dziekuje bardzo!

Mila:

damian: a dlaczego w tej pochodnej V'(H) zmieniamy tylko to w nawiasie a to przed nawiasem zostaje tak jak w V(H)?