Granica funkcji
Michał: Oblicz granicę:
Po podzieleniu przez x
2 zostaje mi x
2 +
x3 i nie wiem czy w takiej postaci mogę
uznać, że funkcja dąży do + nieskończoności. Bo jeśli podzielę przez kolejny x wówczas funkcja
będzie dążyć do − nieskończoności, a to jest sprzeczne z odpowiedziami.
7 mar 11:12
Jerzy:
| | 3x4 + x3 − 18 | |
Zatem licz granicę: limx→−∞ ( |
| ) |
| | 3 | |
7 mar 11:19
'Leszek: Nic nie dziel , widac wyraznie ze dla x →− ∞ to wyrazenie → + ∞
7 mar 11:19
Michał: Dziękuję Jerzy.
@'Leszek
Może i widać, ale na maturze nie napiszę samej odpowiedzi z podpisem "widać". Wolę się
dowiedzieć jak coś rozpisać niż potem gdzieś stracić punkty.
7 mar 11:21
Jerzy:
Teraz wyrażnie widać, że licznik dąży do + ∞
7 mar 11:21
Tadeusz:
ciekawe rzeczy wypisujesz

7 mar 11:22
Jerzy:
W jakim sensie "ciekawe" ?

7 mar 11:23
Tadeusz:
to nie do Ciebie .. to miało być do
Michała 
7 mar 11:24
Michał: Jeśli jeszcze można − granica prawo− i lewostronna:
7 mar 11:25
Jerzy:
A ... OK.

7 mar 11:25
Jerzy:
Ustal po jakich wartościach mianownik zmierza do 0.
7 mar 11:26
Michał: Chodzi o pierwszą czy drugą wypowiedź? Cóż, możliwe że plotę głupoty, bo już trochę nie robiłem
tego typu zadań.
7 mar 11:26
'Leszek: Michal ,wobec tego wykaz na podstawie definicji graniczy funkcji dla x →− ∞ ,ze f(x) →+ ∞.
Nikt wowczas nie bedzie mial watpliwosci .
7 mar 11:27
Jerzy:
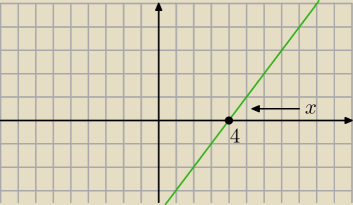
7 mar 11:27
Jerzy:
Podeprzyj sie twierdzeniem,że granica wielomianu stopnia parzystego ( przy a > 0),
wynosi + ∞ ( przy x → +/− ∞)
7 mar 11:29
'Leszek: O wlasnie p.Jerzy podal najlepszy i najkrotszy sposob dla tej graniczy !
7 mar 11:31
Michał: Przepraszam, chciałbym wiedzieć czy dobrze rozumuję:
Licznik będzie zawsze ujemny, ponieważ maksymalną wartością funkcji jest 5, a x ∊(−
∞; 5) x − 6
< 0 jest zawsze prawdą.
Mianownik z kolei będzie zawsze dodatni. I z tego mogę powiedzieć, że granicą funkcji będzie
−
∞. Dobrze myślę?
7 mar 11:40
Jerzy:
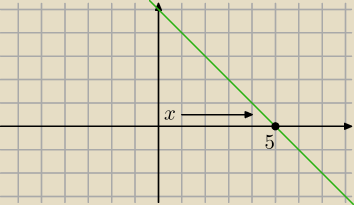
x zmierza do 5 po wartościach dodatnich , licznik jest ujemny, czyli: lim = −
∞
7 mar 11:43
Jerzy:
Nie x zmierza po wartościach dodatnich, tylko mianownik zmierza do 0 po wartościach
| | −1 | |
dodatnich , czyli lim = [ |
| ]= − ∞ |
| | 0+ | |
7 mar 11:45
Michał: | | x + 7 | |
Czyli taki przykład limx→ −3+ |
| mogę zapisać jako |
| | (x+3)(x+4) | |
7 mar 11:53
Jerzy:
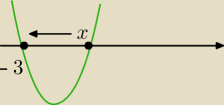
Po jakich wartościach mianownik zmierza do 0 ?
7 mar 11:58
Jerzy:
Sorry ...zły rysunek , tak mianownik zmierza do zera po wartościach dodatnich, lim = +∞
7 mar 12:00
Michał: Bardzo dziękuję za pomoc. Miłego dnia życzę.

7 mar 12:01





 x zmierza do 5 po wartościach dodatnich , licznik jest ujemny, czyli: lim = −∞
x zmierza do 5 po wartościach dodatnich , licznik jest ujemny, czyli: lim = −∞
 Po jakich wartościach mianownik zmierza do 0 ?
Po jakich wartościach mianownik zmierza do 0 ?
