Ostatnie zadanie z konkursu matematycznego dla szkół średnich etap szkolny.
Radek: Na bokach BC i CD kwadratu ABCD dane są punkty K i H odpowiednio w taki sposób, że |KC|=2|KB|
i |HC|=|HD|. Udowodnij równość kątów AKB i AKH.
6 mar 19:13
Adamm:
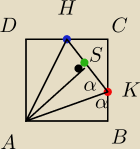
trójkąty ASK oraz ABK są przystające kbk
6 mar 19:30
Adamm: cofam to, zaznaczyłem kąty jako równe na rysunku i dlatego tak napisałem
6 mar 19:30
Adamm: moja propozycja: obliczyć boki |HK|, |AK|, |AH| z tw. Pitagorasa
z tw. Cosinusów wykazać że cosinusy kąta AKB oraz kąta AKH są równe
6 mar 19:36
Kacper:

6 mar 20:11
Radek: Pomimo wszelkich starań nie chce wyjść

|AK|=x
√13
|KH|=x
√3,25
|AH|=x
√11,25
Tw cosinusów:
9x
2=4x
2+13x
2−4x
2√13cosα
11,25x
2=13x
2+3,25x
2−13x
2cosα
9x
2=17x
2−4x
2√13cosα
11,25x
2=16,25x
2−13x
2cosα
4x
2√13cosα=8x
2
13x
2cosα=5x
2
dzielimy przez x
2 i zostaje:
4
√13cosα=8
13cosα=5
Jeśli ktoś widzi błąd lub jakieś

czy też błędy kardynalne to proszę zgłaszać

ale
na konkursie nie można było mięć żadnych kalkulatorów więc wydaje mi się, że musi być inne
dużo prostsze wyjście
6 mar 20:24
Adamm: to jest bardzo proste podejście
a kalkulatora nie potrzeba do tak prostych obliczeń
6 mar 20:28
Radek: | | 5 | | 2√13 | |
proste nie proste ale |
| ≠ |
| :c |
| | 13 | | 13 | |
6 mar 20:31
Radek: Na bokach BC i CD kwadratu ABCD obrano punkty E i F tak, że |EC| = 2|EB| i |FC| = |FD|, Wykaż,
że kąt AEB i kąt AEF są równe. Szukajcie w google a znajdziecie ^^
6 mar 20:57
Eta:
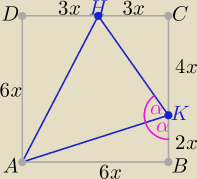
|AK|
2=20x
2 , |KH|
2=25x
2 , |AH|
2= 45x
2
| | 2x | | 1 | |
w ΔABK cosα= |
| = |
| |
| | 2√10x | | √10 | |
w ΔAKH z tw. kosinusów
| | 25x2+20x2−45x2 | | 1 | |
cosα= |
| = ....... = |
| |
| | 2*5x*2√10x | | √10 | |
6 mar 21:06
 trójkąty ASK oraz ABK są przystające kbk
trójkąty ASK oraz ABK są przystające kbk

 |AK|=x√13
|KH|=x√3,25
|AH|=x√11,25
Tw cosinusów:
9x2=4x2+13x2−4x2√13cosα
11,25x2=13x2+3,25x2−13x2cosα
9x2=17x2−4x2√13cosα
11,25x2=16,25x2−13x2cosα
4x2√13cosα=8x2
13x2cosα=5x2
dzielimy przez x2 i zostaje:
4√13cosα=8
13cosα=5
|AK|=x√13
|KH|=x√3,25
|AH|=x√11,25
Tw cosinusów:
9x2=4x2+13x2−4x2√13cosα
11,25x2=13x2+3,25x2−13x2cosα
9x2=17x2−4x2√13cosα
11,25x2=16,25x2−13x2cosα
4x2√13cosα=8x2
13x2cosα=5x2
dzielimy przez x2 i zostaje:
4√13cosα=8
13cosα=5
 czy też błędy kardynalne to proszę zgłaszać
czy też błędy kardynalne to proszę zgłaszać  ale
na konkursie nie można było mięć żadnych kalkulatorów więc wydaje mi się, że musi być inne
dużo prostsze wyjście
ale
na konkursie nie można było mięć żadnych kalkulatorów więc wydaje mi się, że musi być inne
dużo prostsze wyjście
 |AK|2=20x2 , |KH|2=25x2 , |AH|2= 45x2
|AK|2=20x2 , |KH|2=25x2 , |AH|2= 45x2