 Witam, mam problem z następującym zadaniem, a konkretnie ze zlokalizowaniem błędu w
rozumowaniu.
"Podstawą ostrosłupa ABCD jest trójkąt równoboczny ABC o boku długości √2. Wszystkie ściany
boczne są równoramiennymi trójkątami prostokątnymi. Punkt P, zsoatł wybrany wewnątrz
ostrosłupa w ten sposób, że wysokości ostrosłupów ABDP, BCDP, ACDP, ABCP opuszczone z
wierzchołka P mają tę samą długość H. Oblicz H."
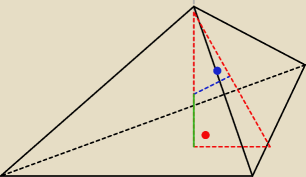
Opiszę rysunek poniżej, aby go nie zaciemnić:
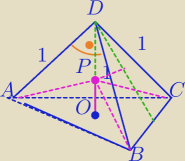
podstawa ABC, wierzchołek D
spodek wysokości O
spodek wysokości ściany bocznej K
Punkt P obrany na wysokości tego ostrosłupa oraz punkt P1 zlokalizowany na wysokości ściany
bocznej (pod kątem prostym)
po obliczeniach:
krawędź ostrosłupa 1
|OK|=√6/6
|DK|=√2/2
|DO|=√3/3
trójkąty DOK i PP1D są podobne z cechy kkk
więc P1P/DP=OK/DO
PP1 stanowi jednocześnie wysokość trójkąta DOK opuszczoną na bok DK
Z równości pól:
OK*DO*1/2=DK*P1P*1/2
P1P=1/3
tu pojawia się problem, ponieważ w oficjalnym zadaniu PP1=H=(3−√3)/6
Będę wdzięczna za oświecenie mnie, bo sama uwikłałam się w swoim rozumowaniu i nie jestem w
stanie odnaleźć tak zwanej "dziury w całym"
Witam, mam problem z następującym zadaniem, a konkretnie ze zlokalizowaniem błędu w
rozumowaniu.
"Podstawą ostrosłupa ABCD jest trójkąt równoboczny ABC o boku długości √2. Wszystkie ściany
boczne są równoramiennymi trójkątami prostokątnymi. Punkt P, zsoatł wybrany wewnątrz
ostrosłupa w ten sposób, że wysokości ostrosłupów ABDP, BCDP, ACDP, ABCP opuszczone z
wierzchołka P mają tę samą długość H. Oblicz H."
Opiszę rysunek poniżej, aby go nie zaciemnić:
podstawa ABC, wierzchołek D
spodek wysokości O
spodek wysokości ściany bocznej K
Punkt P obrany na wysokości tego ostrosłupa oraz punkt P1 zlokalizowany na wysokości ściany
bocznej (pod kątem prostym)
po obliczeniach:
krawędź ostrosłupa 1
|OK|=√6/6
|DK|=√2/2
|DO|=√3/3
trójkąty DOK i PP1D są podobne z cechy kkk
więc P1P/DP=OK/DO
PP1 stanowi jednocześnie wysokość trójkąta DOK opuszczoną na bok DK
Z równości pól:
OK*DO*1/2=DK*P1P*1/2
P1P=1/3
tu pojawia się problem, ponieważ w oficjalnym zadaniu PP1=H=(3−√3)/6
Będę wdzięczna za oświecenie mnie, bo sama uwikłałam się w swoim rozumowaniu i nie jestem w
stanie odnaleźć tak zwanej "dziury w całym"
 Z treści wynika, że
1) H=r − promień kuli wpisanej w ten ostrosłup
Związek V i r :
Z treści wynika, że
1) H=r − promień kuli wpisanej w ten ostrosłup
Związek V i r :
| 1 | ||
V= | *r*P | |
| 3 |
| 1 | 1 | 1 | ||||
V= | *( | *1*1)*1= | ||||
| 3 | 2 | 6 |
| (√2)2*√3 | 1 | |||
P= | +3* | *1*1 | ||
| 4 | 2 |
| 3+√3 | ||
P= | ||
| 2 |
| 1 | 1 | 3+√3 | |||
= | * | *r | |||
| 6 | 3 | 2 |
| 1 | ||
r= | ||
| 3+√3 |
| 3−√3 | ||
r=H= | ||
| 6 |


