 Mam takie zadanka:
1. Wykaż, że jeżeli r jest długością okręgu wpisanego w trójkąt o bokach a,b,c to suma
Mam takie zadanka:
1. Wykaż, że jeżeli r jest długością okręgu wpisanego w trójkąt o bokach a,b,c to suma
| 1 | 1 | 1 | ||||
wysokości w tym trójkącie jest równa r(a+b+c)( | + | + | ). | |||
| a | b | c |
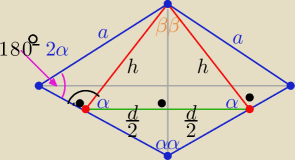
 3. Z wierzchołka rozwartego rombu poprowadzono dwie wysokości. Długość wysokości jest równa h,
a odległość między spodkami tych wysokości równa d. Oblicz pole rombu.
4. Udowodnij, że jeżeli wielomian f(x)= ax3+bx2+cx+d o współczynnikach całkowitych przyjmuje
dla x=0 i dla x=1 wartości nieparzyste, to równanie f(x)=0 nie ma pierwiastków całkowitych.
5. Dany jest czworokąt ABCD wpisany w okrąg. Dwusieczne dwóch przeciwległych kątów tego
czworokąta przecięły ten okrąg w punktach E i F. Wykaż, że odcinek EF jest średnicą tego
okręgu.
(podejrzewam że trzeba znaleźć kąt prosty leżący na EF, ale nie widzę jakoś
3. Z wierzchołka rozwartego rombu poprowadzono dwie wysokości. Długość wysokości jest równa h,
a odległość między spodkami tych wysokości równa d. Oblicz pole rombu.
4. Udowodnij, że jeżeli wielomian f(x)= ax3+bx2+cx+d o współczynnikach całkowitych przyjmuje
dla x=0 i dla x=1 wartości nieparzyste, to równanie f(x)=0 nie ma pierwiastków całkowitych.
5. Dany jest czworokąt ABCD wpisany w okrąg. Dwusieczne dwóch przeciwległych kątów tego
czworokąta przecięły ten okrąg w punktach E i F. Wykaż, że odcinek EF jest średnicą tego
okręgu.
(podejrzewam że trzeba znaleźć kąt prosty leżący na EF, ale nie widzę jakoś  )
)

| d | ||
3/ P=a*h . cosα= | to sinα= √1−cos2α=.... | |
| 2h |
| h | h | h | ||||
sin(180o−2α)=sin(2α)= | ⇒ a= | = | ||||
| a | sin(2α) | 2sinα*cosα |
| h2 | ||
P= | =............. | |
| 2sinα*cosα |

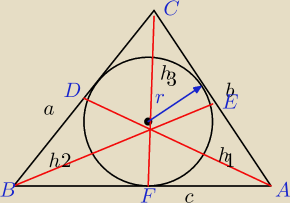 Co do zadania nr 1 to mysle zeby wykorzystac wzory
Co do zadania nr 1 to mysle zeby wykorzystac wzory
| 2p | ||
r= | ||
| a+b+c |
| 1 | 2P | |||
P = | a*h1 to h1= | |||
| 2 | a |
| 1 | 2P | |||
P= | b*h2 to h2= | |||
| 2 | b |
| 1 | 2P | |||
P= | c*h3} to h3= | |||
| 2 | c |
| 2P | ||
r= | ma byc bo p to oznaczenie polowy obwodu | |
| a+b+c |

 Może za rok...
Może za rok...  Dziękuję 5−latek
Dziękuję 5−latek 