Trygonometria Kajtek: Gdzie tutaj robię błąd? Setny raz i nie wychodzi Podaj rozwiązania nierówności należące do przedziału <0; 2π>

	π
2sin(x+		) ≥ 1 /:(2)
	3

	π		1
sin(x+		) ≥
	3		2

	π
podst. t = (x+		)
	3

	π		−π
t1 =		+ 2kπ, czyli x1 =		+ 2kπ
	6		6

	5π		π
t2 =		+ 2kπ, czyli x2 =		+ 2kπ
	6		2

Kajtek:

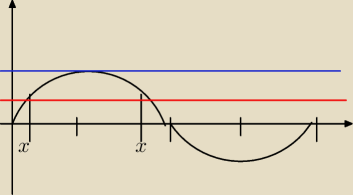
	−π		π
x1 i x2 oznaczone kolejno, czyli wynikiem równania są x ∊ <		;		>, a odpowiedź to
	6		2

	π		11π
x ∊ <0;		> ∪ <		; 2π>
	2		6

'Leszek: w treści zadania jest napisane x ∊< 0,2π> tego nie uwzględniłeś

Mila:

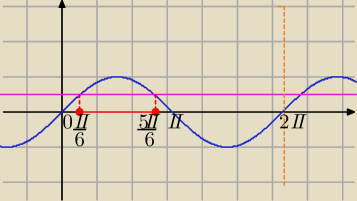
	π		1
sin(x+		)≥		i x∊<0,2π>
	3		2

π		π		5π		π
	+2kπ≤x+		≤		+2kπ / −
6		3		6		3

	π		3π
−		+2kπ<x<		+2kπ
	6		6

k=0 i x∊<0,2π>

	π
x>0 i x<
	2

============== k=1 i x∊<0,2π>

	11π
x>		i x<2π
	6

========== zaznacz sobie na osi liczbowej przedziały dla k=0 i k=1.

Kajtek: Dzięki wielkie, rzeczywiście. Już widzę błąd

Mila: