funkcje
ewa: Dana jest funkcja: f(x) = √|2−x| −3 − √6−|2x−4|
a) wyznacz dziedzinę tej funkcji
b) podaj zbiór wartości
c) sporządź wykres
19 sty 17:28
ewa: 

19 sty 19:05
bb: df= x:x∊{−1;5}
Zw= y:y∊{0}
wykresu nie rysuje
19 sty 19:55
ewa: bb mógłbyś mi wyjaśnić jak to wogóle wyliczyłeś

19 sty 19:57
bb: a) chcąc policzyc df to rozwiązujesz nierówności |2−x|−3≥0 i 6−|2x−4|≥0 bo tak mówi definicja
pierwiastka, po rozwiązaniu nierowności bierzesz część współna i wychodzi dziedzina
b) punkty −1 oraz 5 podstawiasz do wzoru funkcji i wychodzi f(−1)=0 oraz f(5)=0 czyli zbiór
wartości piszesz jak wyzej w poprzedniej odpowiedzi
19 sty 20:02
ewa: tylko ze jest tu wartosc bezwzgledna.. wiec rozwiazuje sie to tak samo

19 sty 21:01
bb: rozwiąż sobie nierówności
−3≥2−x≥3 i 6≥2x−4≥−6
19 sty 22:25
ewa: mogłby ktos jeszce sprawdzic to zad czy aby napewno jest dobrze

? PROSZE
20 sty 20:08
Julek:
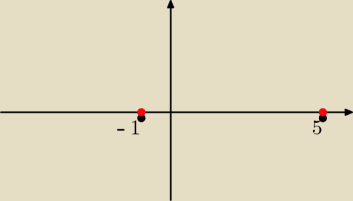
a)
|2−x| ≥ 3
2−x ≥ 3 ∨ 2−x ≤ −3
−1 ≥ x ∨ 5 ≤ x
x∊(−∞; −1> ∪ <5;+∞)
|2x−4| ≤ 6
2x−4 ≤ 6 ∧ 2x−4 ≥ − 6
x≤5 ∧ x ≥ −1
część wspólna, więc D: x∊{−1; 5}
b)
f(x) =
√|2−x| −3 −
√6−|2x−4|
f(−1) = 0
f(5) = 0
Zw = 0
c) te dwie przepiękne kropki na rysunku

20 sty 20:19
Julek: c) (czerwone)
20 sty 20:19
ewa: i nie bedzie tu lini skoro wykres

? dziekuje slicznie teraz mi sie wszytsko wyjasnilo juz

20 sty 20:26
ewa: 

20 sty 20:48
Julek:
Wykresem może być naprawdę wszystko, nawet penis (tylko wtedy to już raczej nie będzie
funkcja

). Wykresem funkcji nie zawsze są linie, mogą to być krzywe, proste, punkty,
parabole itp. Najważniejsze, aby dla jednego X nie przyjmowało różnych Y (wtedy można to
nazwać funkcją).
Wykres funkcji
f(x) =
√|2−x| −3 −
√6−|2x−4|
jest dobry
20 sty 21:07
ewa: aha to tego nie wiedzilam ze pkt moga byc wykresem... dziekuje jeszxcze raz za wytlumaczenie

20 sty 21:09
ewa: pomocy

w równaniach napisanych przez Julek raz jest ∧ a raz v i ktore ma byc wkoncu

27 sty 11:08
ewa: teraz po jeszcze jednej analizie wydaje sie mi ze nbadal jest tu cos zle....
poniewaz do −1 ≥ x ∨ 5 ≤ x
przedzial nie bedzie tak wygladal x∊(−∞; −1> ∪ <5;+∞)
prosze o sprawdzenie

27 sty 11:16
ewa: tylko bedzie x∊ <−1, 5>

27 sty 11:17
ewa: i z drugiego rownania rezdzial bedzie taki sam.. wiec dziedzina bedzie wygladac D: x∊<−1, 5> ?
i wykres również bedzie inny.. zgadza sie czy jestem w bledzie

27 sty 11:19
Bogdan:
ewo, jesteś w błędzie, rozwiązanie Julka jest poprawne.
27 sty 11:43
ewa: to w 2 równaniu x∊

i jeszcze jakbys mogl mi powiediec co z tymi znakami

∧ i v

tez sa
poprawnie

27 sty 11:46
Bogdan:

|2 − x| − 3 ≥ 0 i 6 − |2x − 4| ≥ 0
|2 − x| ≥ 3 i |2x − 4| ≤ 6
(2 − x ≤ −3 lub 2 − x ≥ 3) i −6 ≤ 2x − 4 ≤ 6 / :2
(x ≥ 5 lub x ≤ −1) i −1 ≤ x ≤ 5
x ∊ {−1, 5}
27 sty 12:01
ewa: czyli u Julka wszedzie ma byc v....
27 sty 12:03
ewa: poprostu czt wg sposobu jakim rozw Julek ma byc tak i czy lub

27 sty 12:05
Julek:
Ewcia, moje rozwiązanie jest dobre.
Gdy rozwiązujesz nierówność modułową np.
|2−x| ≥ 3
to obracasz znak nierówności o 90o w prawo, czyli tu będzie
∨
zaś gdy masz np.
|2−x| ≤ 3 to znak ten wygląda
∧
27 sty 12:14




 ? PROSZE
? PROSZE
 a)
|2−x| ≥ 3
2−x ≥ 3 ∨ 2−x ≤ −3
−1 ≥ x ∨ 5 ≤ x
x∊(−∞; −1> ∪ <5;+∞)
|2x−4| ≤ 6
2x−4 ≤ 6 ∧ 2x−4 ≥ − 6
x≤5 ∧ x ≥ −1
część wspólna, więc D: x∊{−1; 5}
b)
f(x) = √|2−x| −3 − √6−|2x−4|
f(−1) = 0
f(5) = 0
Zw = 0
c) te dwie przepiękne kropki na rysunku
a)
|2−x| ≥ 3
2−x ≥ 3 ∨ 2−x ≤ −3
−1 ≥ x ∨ 5 ≤ x
x∊(−∞; −1> ∪ <5;+∞)
|2x−4| ≤ 6
2x−4 ≤ 6 ∧ 2x−4 ≥ − 6
x≤5 ∧ x ≥ −1
część wspólna, więc D: x∊{−1; 5}
b)
f(x) = √|2−x| −3 − √6−|2x−4|
f(−1) = 0
f(5) = 0
Zw = 0
c) te dwie przepiękne kropki na rysunku 
 ? dziekuje slicznie teraz mi sie wszytsko wyjasnilo juz
? dziekuje slicznie teraz mi sie wszytsko wyjasnilo juz 


 ). Wykresem funkcji nie zawsze są linie, mogą to być krzywe, proste, punkty,
parabole itp. Najważniejsze, aby dla jednego X nie przyjmowało różnych Y (wtedy można to
nazwać funkcją).
Wykres funkcji
f(x) = √|2−x| −3 − √6−|2x−4|
jest dobry
). Wykresem funkcji nie zawsze są linie, mogą to być krzywe, proste, punkty,
parabole itp. Najważniejsze, aby dla jednego X nie przyjmowało różnych Y (wtedy można to
nazwać funkcją).
Wykres funkcji
f(x) = √|2−x| −3 − √6−|2x−4|
jest dobry

 w równaniach napisanych przez Julek raz jest ∧ a raz v i ktore ma byc wkoncu
w równaniach napisanych przez Julek raz jest ∧ a raz v i ktore ma byc wkoncu



 i jeszcze jakbys mogl mi powiediec co z tymi znakami
i jeszcze jakbys mogl mi powiediec co z tymi znakami ∧ i v
∧ i v  tez sa
poprawnie
tez sa
poprawnie
 |2 − x| − 3 ≥ 0 i 6 − |2x − 4| ≥ 0
|2 − x| ≥ 3 i |2x − 4| ≤ 6
(2 − x ≤ −3 lub 2 − x ≥ 3) i −6 ≤ 2x − 4 ≤ 6 / :2
(x ≥ 5 lub x ≤ −1) i −1 ≤ x ≤ 5
x ∊ {−1, 5}
|2 − x| − 3 ≥ 0 i 6 − |2x − 4| ≥ 0
|2 − x| ≥ 3 i |2x − 4| ≤ 6
(2 − x ≤ −3 lub 2 − x ≥ 3) i −6 ≤ 2x − 4 ≤ 6 / :2
(x ≥ 5 lub x ≤ −1) i −1 ≤ x ≤ 5
x ∊ {−1, 5}
