Proszę o pomoc Gapa32: Dany jest półokrąg. Rozpatrzmy trzy równoległe pomiędzy sobą cięciwy tego półokręgu – a, b, c. Odległość pomiędzy cięciwami a i b jest równa odległości pomiędzy cięciwami b i c. Ponadto, długości cięciw a, b, c wynoszą odpowiednio 26, 22 i 14. Ile wynosi promień danego półokręgu?

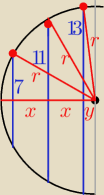
Janek191: 7² + (2 x + y)² = r² 11² + (x + y)² = r² 13² + y² = r² 49 + 4 x² + 4 x y + y² = r² 121 + x² + 2 x y + y² = r² / *(−2) 169 + y² = r² ⇒ y² = r² − 169 49 + 4 x² + 4 x y + r² − 169 = r² − 242 − 2 x² − 4 x y − 2 r² + 338 = − 2 r² 49 + 4 x² + 4 x y = 169 −242 −2 x² − 4 x y = − 338 −−−−−−−−−−−−−−−−−−− dodajemy stronami − 193 +2 x² = − 169 2 x² = 24 x² = 12 x = 2√3 ======== więc 4* 12 + 4*2√3 y = 120 8√3 y = 72 √3 y = 9 y = 3 √3 ======== zatem 13² + y² = r² r² = 169 + 27 = 196 r = 14 ======

Gapa32: Dzięki wielkie