X 1q: Zbadaj wzajemne położenie okręgów o podanych równaniach Napisz równania prostych będących osiami symetrii figury utworzonej z tych okręgów X² + (y−2)² =4 i (x +3 )³ + (y−3)²=17

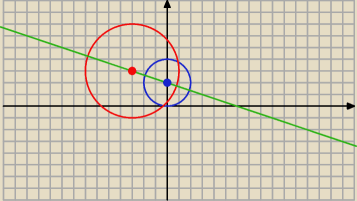
Janek191: S₁ = ( 0, 2) S₂ = ( − 3, 3)

	3 −2		1
y =		x + b = −		x + b S1 = ( 0, 2)
	− 3 − 0		3

więc 2 = b

	1
Odp. y = −		x + 2
	3

======================

Janek191: cd. I S₁ S₂ I = √(−3)² + 1² = √10 < r₁ + r₂ = 2 + √17 więc okręgi się przecinają,