analityczna moniczka: Odcinek AB o koncach A(8, −2) i B(−8,6) jest przeciwprostokątna trójkata prostokatnego AB Spodek D wysokosci poprowadzonej z wierzchołka C dzieli przeciwprostokątna na odcinki AD I DB takie, ze |AD|: |DB|=5:3 wyznacz wierzchółek C

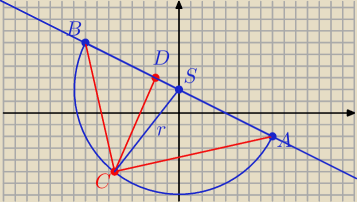
Janek191: I AB I = √16² + 8² = √256 + 64 = √320 = √16*4*5 I AB I = 8 √5 8 x = 8 √5 x = √5 r = 4 x = 4√5 ============ h² = 3 x * 5 x = 15 x² h = √15 x = √15* √5 = √25*3 = 5√3 S = ( 0, 2) − środek odcinka AB D = ( − 2, 3) C = ( a, b) ( a + 2)² + ( b − 3)² = 75 a² + ( b − 2)² = 80 a² + 4 a + 4 + b² − 6 b + 9 = 75 a² + b² − 4 b + 4 = 80 −−−−−−−−−−− odejmujemy stronami 4a + 13 −2 b = − 5 4 a − 2 b = − 18 2 a − b = − 9 b = 2a + 9 zatem a² + ( 2 a + 9 − 2)² = 80 a² + 4 a² + 28 a + 49 = 80 5 a² + 28 a − 31 = 0 Δ = 784 + 620 = 1 404 √Δ = 6√39

	− 28 − 6√39
a =		= −2,8 −0,6 √39
	10

b = − 5,6 − 1,2 √39 + 9 = 3,4 − 1,2 √39 C = ( −2,8 − 0,6 √39 ; 3,4 − 1,2 √39)

'Leszek: Duzo prosciej robi sie to zadanie na wektorach Wektor AB = [ −16 , 8 ] , wewktor AD = (5/8) *AB ⇒ AD = [ −10 , 5 ] oraz AD = [ x−8 , y +2] ⇒ D(−2,3) Wyznaczam prosta AB : y − 0,5 x + 2 Prosta DC : y = 2x +7 ( bo prostapadla do AB) Punkt C( x , 2x +7) Wektor CB = [ −8 −x , 6 − 2x −7] , wektor CA= [ 8 −x ,−2 − 2x −7] I korzystamy z iloczynu skalarnego wektorow CA o CB = 0 .