geometria analityczna Ilona: W trójkącie prostokątnym ABC (kąt B=90) dwa wierzchołki mają współrzędne A(4,−5) i C (−8,5). Wyznacz współrzędne wierzchołka B wiedząc, że pole trójkąta ABC jest równe 61. Znalazłam gdzieś, że to jest trójkąt równoramienny − wtedy wydaje się to proste. Tylko skąd wiemy , że jest prostokątny i równoramienny jednocześnie?

Ilona: up − dlaczego trójkąt ABC jest równoramienny?

Antonni: A dlaczego na starcie zakladasz ze to trojkat rownoramienny ? Moze znajac pole nalezy policzyc jego wysokosc Masz wtedy odlegosc punktu B od prostej AC

Ilona: i co dalej? Nie mam prostej na której leży B. Zatem będzie nadal zawierał dwie niewiadome x i y. Podstawiając do wzoru na odległość punktu B od prostej AC nadal będą dwie niewiadome x i y.

Ilona: Chyba wiem. Trzeba napisać równanie prostej równoległej do AC oddalonej od niej o h. Wtedy będzie prosta zawierająca B.

Antonni: Dlugosc odcinka AC= √244= 2√61 jest to dlugosc przeciwprostokatnej tego trojkata

	p		61
wysokosc h =		=		= √61
	0,5*AC		√61

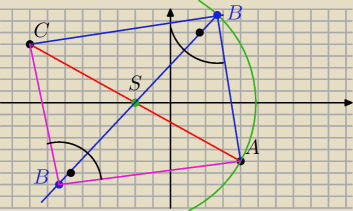
Teraz dopiero z tego mozemy wnioskowac ze ten trojkata jest rownoramienny Srodek okregu opisanego na trojkacie prostokatnym lezy w polowie przeciwprostokatnej czyli promien tego okregu na dlugosc R= √61 Wysokosc tez ma dlugosc h=√61 Wiec podzieli ona przeciwprostokatna na dwie rowne czesci To jest szkic do zadania i zobacz ze beda takie dwa punkty B

Antonni: I tak mozesz zrobic jak piszsesz 1> Wyznaczyc proste rowno;egle do AC i oddalone o √61 od niej ze wzoru

	|C−C1|
d=
	√A2+B2

Wyznaczysz wspolczynnik C₁ prostych rownoleglych (beda dwie Z tym ze rownanie prostej AC doprowadzisz do postaci ogolnej i masz wspolczynniki A B i C 2. Z tego ze to jest trojkat rownoramienny wyznaczysz srodek ZC i piszsesz rownanie prostej prostopadlej do AC i przechodzacej przez srodek 3> Wyznaczasz punkty przeciecia tych prostych rownoleglych z prosta prostopadla 4> Koniec zadania