hmm
cynamonek:
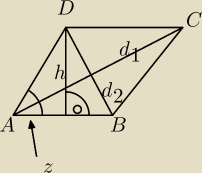
wysokość DE rombu ABCD opuszczona na bok AB podzieliła ten bok na odcinki, których stosunek
długości wynosi 1:3. Dlugość wysokości DE jest równa
√5. Oblicz dlugość przekątnych rombu
ABCD
mogę przyjąć, że z ma 30
0 ?
5 mar 16:49
Mila:
A dlaczego tak chcesz przyjąć?
5 mar 16:56
cynamonek: Bo nie wiem od czego tutaj mogę zacząć. A mam podaną wysokość w tym trójkącie to starałbym się
z tego trójkąta prostokątnego robić coś. Chyba, że z drugiego trójkąta prostokątnego który
jest już przekątną; )

5 mar 17:02
Adamm: najpierw może policz bok rombu z twierdzenia Pitagorasa
5 mar 17:03
Adamm: i trzeba rozpatrzyć 2 przypadki bo w zadaniu nie jest podane jak dzieli ten bok
5 mar 17:05
cynamonek: czyli mogę zrobić to −a2 + 12 a +5 = 0 tak wyliczam ten bok?
5 mar 17:08
cynamonek: 13a w sumie
5 mar 17:13
'Leszek: Jezeli AE = (1/3)a to dla Δ AED tw . Pitagorasa : a2 = (1/9)a2 + 5 ⇒ a= √2,5
i.t.d
5 mar 17:22
cynamonek: a pytanie mam bo obliczylem juz ale wzialem 14 to nie powinienem brać 1/4? bo 1 długość i
3 długości czyli w sumie 4 części?
5 mar 17:31
'Leszek: Tak ,moj blad ,masz racje !
5 mar 17:36
cynamonek: Czyli a = 4 √33 a jak to podkładam do kolejnego trójkąta prostokątnego to nie wychodzi
mi nic? Gdzie tutaj jest błąd?
5 mar 19:54
cynamonek: dobra dzięki nie odświeżyłem

5 mar 20:00
cynamonek: czemu w drugim wersie jest 14 a nie 15 ?
5 mar 20:05
Mila:
Zaraz napiszę.
5 mar 20:08
Mila:
Masz odpowiedź do zadania?
5 mar 20:16
Mila:
Mam błąd w rachunkach, liczę.
5 mar 20:17
Mila:
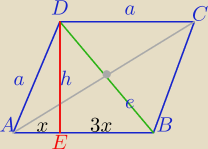
h=
√5
P=a*
√5
1)
W ΔAED:
2)
Z tw. cosinusów
| | 3 | | √3 | | √3 | | 4√3 | |
|DB|2= |
| a2⇔ |DB|= |
| *a= |
| * |
| |
| | 2 | | √2 | | √2 | | 3 | |
|DB|=2
√2
=======
( to samo wyjdzie z tw. Pitagorasa w ΔDEB:
|DB|
2=
√52+(
√3)
2⇔|DB|
2=8
|DB|=2
√2 )
3)
========
5 mar 20:45
cynamonek: teraz się zgadza

wychodziło właśnie mi tak samo a jak teraz i myślałem, że źle robie

5 mar 20:51
cynamonek: dziękuje

5 mar 20:52
Mila:

5 mar 20:53
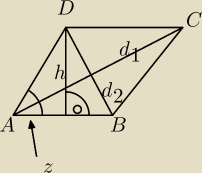 wysokość DE rombu ABCD opuszczona na bok AB podzieliła ten bok na odcinki, których stosunek
długości wynosi 1:3. Dlugość wysokości DE jest równa √5. Oblicz dlugość przekątnych rombu
ABCD
mogę przyjąć, że z ma 300 ?
wysokość DE rombu ABCD opuszczona na bok AB podzieliła ten bok na odcinki, których stosunek
długości wynosi 1:3. Dlugość wysokości DE jest równa √5. Oblicz dlugość przekątnych rombu
ABCD
mogę przyjąć, że z ma 300 ?


 h=√5
P=a*√5
1)
W ΔAED:
h=√5
P=a*√5
1)
W ΔAED:
 wychodziło właśnie mi tak samo a jak teraz i myślałem, że źle robie
wychodziło właśnie mi tak samo a jak teraz i myślałem, że źle robie 

