Obicz maksymalną objętość stożka Karol: Obwód trójkąta równoramiennego wynosi 2p. Jaką długość powinny mieć boki tego trójkąta aby objętość bryły powstałej przez obrót trójkąta dokoła jego osi symetrii była największa?

Karol: Proszę o jakieś wskazówki co do pochodnej

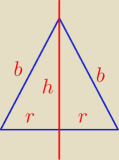
Janek191: 2 r + 2 b = p ⇒ 2 b = p − 2 r ⇒ b = 0,5 p − r b² = 0,25 p² − p*r + r²} h = √ b² − r²

	1		1		1
V =		π r2*h =		π r2*√b2 − r2 =		π r2*√0,25 p2 − p*r
	3		3		3

	1
V(r) =		π √ 0,25 p2 r4 − p*r5
	3

więc

	1		p2 r3 − 5p*r4
V '(r) =		π *		= 0 ⇔ p2 r3 = 5 p r4
	3		2 √ 0,25 p2 r4 − p*r5

p = 5 r r = 0,2 p więc a = 2 r = 0,4 p b = 0,3 p ========

Janek191: Pomyłka zamiast 2p wpisałem p