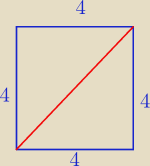
Blagam o obliczenia Olka i Piotrek: Przekątna prostokąta długości 4√2 tworzy z bokiem tego prostokąta kat 45 st. Pole tego prostokąta jest równe: A. 32 B. 64 C. 16√2 D. 16

Jerzy: To kwadrat.

Jerzy: a√2 = 4√2 ⇔ a = 4 P =a² = 4² = 16

Janek191: P = 0,5*(4√2)² = 0,5*32 = 16 lub P = 4² = 16

Olka i Piotrek: A może być tak obliczone sin 45 i z własności 45 stopni?

Jerzy: Może.

Olka i Piotrek: Pomzecie dalej?

Jerzy:

a		√2		8
	= sin450 ⇔ a = d*sin450 = 4√2*		=		= 4
d		2		2

Olka i Piotrek: Rozwiązaniem równania |4x+1|=5 są liczby A. 1 i −1.5 B. −1 i 1.5 C. −4, 4 D. −2.5 i 1

Olka i Piotrek: Z innym zadaniem w sensie

Jerzy: To wrzucaj.

Olka i Piotrek: Jest wyżej

Jerzy: |4x+1I = 5 ⇔ 4x+1 = 5 lub 4x+1 = −5 ..... i licz dalej.

Olka i Piotrek: To będzie ODP A.

Jerzy: Tak.

Olka i Piotrek: To jeszcze Funkcja f określona jest wzorem f(x)x²−6x+9. Wówczas punkt p=(3,0): a) leży powyżej wykresu tej funkcji b) jest wierzchołkiem paraboli będącej wykresem tej funkcji c) jest punktem przecięcia wykresu tej funkcji z osią Y d) leży poniżej wykresu tej funkcji.

Jerzy: Odp: b)

	6
xw =		= 3
	2

y_w = f(3) = 0

Olka i Piotrek: Delty nie trzeba liczyć?

Jerzy: A po co ?

Olka i Piotrek:

	4x
Do dziedziny funkcji określonej wzorem f(x)=		nie należą liczby 3 i −2. Wynika
	(x−a)(x−3)

z tego ze liczba a jest równa: A. 3 B. −3 C. 2 D.−2

Olka i Piotrek: Nie wiem w sumie

Jerzy: a = −2 , bo: − 2 − (−2) = −2 + 2 = 0

Olka i Piotrek: Nie rozumiem

Jerzy: Jeśli a = −2 to masz w mianowniku (x+2) , a ten nawias się zeruje dla: x = −2, czyli liczba x = −2 nie należy do dziedziny.

Olka i Piotrek: Napisz mi to teraz liczbami

Jerzy: Dla jakiego x wyrażenie : x + 2 jest równe 0 ?

Olka i Piotrek: X=−2

Jerzy: Zatem x = −2 nie należy do dziedziny.

Olka i Piotrek: Miary kątów trójkąta tworzą ciąg arytmetyczny a_n i różnicy r. Wynika z tego ze:

	a1
A. A1−r=60 st B. A1+r=60 st C.		=60 st D. A1*r=60 st
	r

Olka i Piotrek: Halo?

Zdzisław: 180^o = α + β + γ 180^o = α + α + r + α + 2r 180^o = 3α + 3r // :3 60^o = α + r ⇒ 60^o = A₁ + r Odpowiedź B.