zad
kkk: Proszę o dokładne wytłumaczenie
Dane są ostrosłupy prawidłowe sześciokątne o krawędzi bocznej długości 8cm. Oblicz krawędź
podstawy tego z ostrosłupów który ma największą objętość
5 mar 09:00
===:
Zacznij od rysunku.
Wyznacz h w zależności od a (z Pitagorasa)
Wyznacz wzór na objętość (niewiadoma a)
Szukaj maximum
5 mar 10:06
g:
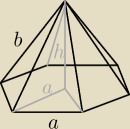
Sześciokątną podstawę można podzielić na 6 trójkątów równobocznych o boku a.
| | a2*√3/4 * h | |
V = 6 * |
| (objętość ostrosłupa) |
| | 3 | |
| | a * a*√3/2 | |
wyrażenie a2*√3/4 to pole pojedynczego trójkąta (= |
| ) |
| | 2 | |
h =
√b2−a2 (wyskość ostrosłupa, b=8)
Wstaw wzór na h do wzoru na V i otrzymasz V w funkcji a. Żeby nie mieć kłopotu
z pierwiastkiem to podnieś obie strony do kwadratu i otrzymasz V
2 w funkcji a
2.
V
2 = (3/4) * (a
2)
2*(b
2−a
2) = (3/4) * c
2*(b
2−c) (c = a
2)
Ta funkcja ma maksimum dla jakiegoś c.
Znajdź to maksimum licząc pochodną i przyrównując ją do zera
(3/4) * [2c*(b
2−c) − c
2] = 0
a = b *
√2/3
5 mar 10:11
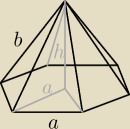 Sześciokątną podstawę można podzielić na 6 trójkątów równobocznych o boku a.
Sześciokątną podstawę można podzielić na 6 trójkątów równobocznych o boku a.