równania boków trójkąta
al: w trójkącie ABC dwie wysokości zawierają się w prostych K: x+y−4=0 oraz l:2x−y=0. Wyznacz
równania ogólne prostych, w których zawierają się boki trójkąta, wiedząc, że A (0,2)
Umiem obliczyć dwie proste: AC(bo jest prostopadła do k) i AB (prostopadła do l), ale co z
trzecią? Proszę o pomoc. AC: x−y+2=0 i AB: x−2y−4=0
4 mar 20:45
===:
wykorzystaj fakt, że wysokości trójkąta przecinają się w jednym punkcie

4 mar 20:51
al: Kurde, tylko jak teraz wykorzystać ten wyliczony punkt przecięcia wszystkich wysokości?

4 mar 21:01
al: coś z prostopadłością BC i AP?
4 mar 21:03
===:
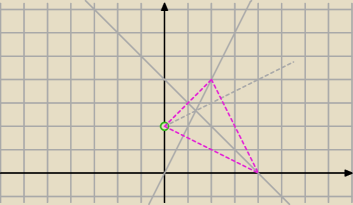
4 mar 21:07
al: dziękuję, zaczęłam od rysunku. Obliczyłam punkt przecięcia wysokości tj. (4/3 , 8/3) i nie
bardzo wiem co dalej
4 mar 21:12
===:
przez punkt A piszesz równanie prostej prostopadłej do prostej 2x−y=0 i szukasz
punktu jej przecięcie z drugą prostą zawierającą wysokość. Ten punkt to wierzchołek.
itd

4 mar 21:16
al: dzięki za pomoc, ale nie zrobię tego i tak

4 mar 21:23
===:
Prosta 2x−y=0 ⇒ y=2x
| | 1 | |
Prostopadła do niej ma współczynnik kierunkowy a=− |
| |
| | 2 | |
| | 1 | |
Równanie prostej przechodzącej przez A i a=− |
| |
| | 2 | |
| | 1 | | 1 | |
y−2=− |
| (x−0) ⇒ y=− |
| x+2 |
| | 2 | | 2 | |
Szukasz punktu przecięcia tej prostej z prostą x+y−4=0 ⇒ y=−x+4
| | 1 | |
masz więc −x+4=− |
| x+2 ⇒ x=4 po podstawieniu x=4 do y=−x+4 |
| | 2 | |
otrzymasz drugą współrzędną y=0
Więc punkt B=(4, 0) jest wierzchołkiem
Wierzchołek C już dla Ciebie

4 mar 21:35





