Geometria Aster: Punkty E i F leża odpowiednio na bokach BC i CD prostokąta ABCD , przy czym trójkąt AEF jest równoboczny. Punkt M jest środkiem odcinka AF. Wykaż że trójkąt BCM również jest równoboczny.

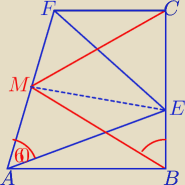
Rafal: Dorysujmy środkową EM. W trójkątach równobocznych środkowe pokrywają się z wysokościami, dwusiecznymi, symetralnymi, symedianami i czymś tam jeszcze, więc kąt EMA jest prosty, a co za tym idzie suma miar kątów ABE i EMA wynosi 180 stopni, co wreszcie oznacza, że punkty A, B, E i M leżą na jednym okręgu. Punkty A i B leżą po tej samej stronie prostej ME, więc z twierdzenia o kątach wpisanych opartych na tym samym łuku mamy, że ∡EBM=∡EAM=60. Spoglądając na czworokąt FCEM, widzimy, że ∡ECM=60. I po dowodzie.

===: ... żaden to dowód. Założyłeś z góry, że ME jest środkową i wysokością. Nie wykazałeś, że ta środkowa jest wysokością.

Rafal: No cóż... Nie ma to jak doczepić się, że w rozwiązaniu ktoś korzysta z faktów oczywistych dla przeciętnego gimnazjalisty.

===: najlepsza forma obrony to atak ... sarkazm ...ale to nie ukrywa twojej głupoty

Rafal: Przepraszam, że w ogóle ośmieliłem się cokolwiek napisać. Powiedz proszę, jak Ty byś to rozwiązał.