Stereometria Michał: Dany jest trójkąt ABC, w którym kąt ACB = 120^o, AB = √31, AC = 1. Trójkąt ten obrócono wokół prostej zawierającej najkrótszy bok. Oblicz objętość otrzymanej bryły. Zadanie rozwiązałem obliczając pola obu stożków, ale na końcu okazało się, że wynik jest błędny, bo powinienem odjąć pole jednego stożka od drugiego zamiast je dodawać tylko nie wiem dlaczego.

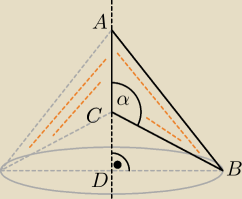Pytający: Trójkąt ABC obracasz wokół AC i to jest Twoja bryła (to pomarańczowe, tylko w 3d). Objętość tej bryły jest równa różnicy objętości stożków otrzymanych poprzez obrót wokół prostej zawierającej |AC| odpowiednio trójkątów ABD oraz BCD. Oznaczmy kolejno objętości brył: V_ABC, V_ABD, V_BCD, wtedy:

	π		π
VABC=VABD−VBCD=		|BD|2(|AD|−|CD|)=		|BD|2|AC|
	3		3

Jak już policzyłeś, |BC|=5.

	5√3
∡BCD=60o, więc |BD|=
	2

Ostatecznie:

	π		5√3		25π
VABC=		(		)2*1=
	3		2		4

Michał: Aaa... Teraz rozumiem dlaczego należy odjąć te pola. Bardzo dziękuję za pomoc.