.,.,
Pełcio: Cześć

Takie zadanka znalazłem:
1. Określ liczbę rozwiązań układu w zależności od parametru a:
2.Znajdź najmniejszą wartość ułamka:
3. Wyznacz wszystkie funkcje liniowe f(x)= ax+b, spełniające warunki
f(a)= 2014
14b oraz f(b)= 2014
14a.
4.Wyznacz wszystkie punkty należące do wykresu funkcji
| | √3x2−12x+16 | |
f(x)= |
| o całkowitych współrzędnych. |
| | √x2−4x+1 | |
moja propozycja to koniunkcja rozwiązań takich nierówności:
3x
2−12x+16≥0 oraz x
2−4x+1>0, nie mam odpowiedzi, więc pytam czy tylko na tym zadanie się
opiera?
5. Oblicz pole figury F, która jest zbiorem wszystkich punktów (x,y) spełniających nierówność:
x
2+y
2≤2(|x|+|y|)
6. Udowodnij, że jeśli liczba 6 i n są względnie pierwsze, to liczba n
4−5n
2+4 jest podzielna
przez 72.
doprowadzam do postaci (n−2)(n−1)(n+1)(n+2) i co dalej?
Chętnie przyjmę jakieś podpowiedzi

4 mar 14:58
Pełcio: W ostatnim n nie dzieli się przez 2 ani 3.
Więc n=3k+1 lub 3k+2, podstawić i mnożyć

4 mar 15:03
Adamm:
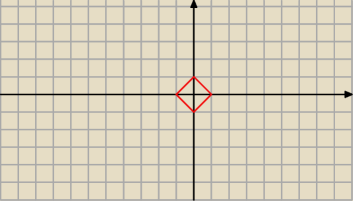
1. graficznie
|y|+|x|=1
|y|=1−|x| dla 1−|x|≥0 czyli 1≥x≥−1
y=1−|x| lub y=|x|−1
dla a>0 mamy
dla
√a=1 mamy 4 rozwiązania
dla
√a=
√2/2 mamy 4 rozwiązania
dla
√a∊(
√2/2;1) mamy 8 rozwiązań
dla reszty brak
4 mar 15:06
3Silnia&6: 6) NWD(n,6) = 1, wiec n jest postaci: 6k + 1 lub 6k + 5 = 6k − 1
Teraz podstawiasz za n=6k+1 v n=6k−1 i do postaci iloczynowej

4 mar 15:12
3Silnia&6: f(b) = 201414a
f(b) = ab + b
ab+b = 201414a ⇔ ab+b − 201414a =0 = (a+1)(b−201414a) = 201414a
4 mar 15:14
Adamm: 3. b(a+1)=2014
14a ∧ a
2+b=2014
14b
a=0 lub a
2+a−(2014
14−1)2014
14=0
niech x=2014
14
Δ=(2x−1)
2
a=2014
14−1 lub a=−2014
14
mamy rozwiązania (a; b)
| | 201428 | |
(0; 0), (201414−1; 201414−1), (−201414; |
| ) |
| | 201414−1 | |
4 mar 15:15
Pełcio: Adamm dziękuję, a możesz jeszcze powiedzieć jak dobierasz te rozwiązania?

Racja
Silnia, dzięki

4 mar 15:15
4 mar 15:18
Pełcio: Dzięki za trzecie, nad pierwszym jeszcze pomyślę.
4 mar 15:31
Adamm:
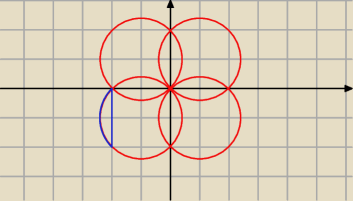
x
2+y
2≤2(|x|+|y|) ⇔ x
2−2|y|+y
2−2|x|≤0 ⇔
⇔ (|x|−1)
2+(|y|−1)
2≤2
dla x≥0 oraz y≥0 mamy koło o środku (1;1) i promieniu
√2
podobnie dla reszty
otrzymujemy rysunek
wyznaczając pole wycinka zaznaczonego na niebiesko dostajemy pole
| | 1 | |
(zauważ że jest on oparty na łuku który jest |
| koła) |
| | 4 | |
4 mar 15:34
Pełcio: Czyli znowu z tego równania okręgu tak?
Też mam pytania do tego:
jeśli mamy to x≥0 i y≥0 to skąd wiesz że to koło o promieniu √2 skoro to jest nierówność a
nie równość?
i jeszcze
skąd wiadomo, że dla reszty tzn:
x≥0 i y<0
x<0 i y≥0
x<0 i y<0
jest tak samo?
4 mar 15:42
Adamm: ale czy to nie jest oczywiste?
skoro okrąg to zbiór punktów równo odległych od środka to koło (zamknięte) to zbiór punktów
równo odległych lub o mniejszej odległości od środka
4 mar 15:51
Pełcio: Tak, to jest, ale zawsze promień będzie równy √2?
4 mar 15:59
Adamm: przecież widzisz że tam jest 2 po prawej
czyli r2=2 czyli r=√2
4 mar 16:03
Adamm: a wyrażenia w kwadratach mówią jedynie o położeniu środka
4 mar 16:03
Pełcio: Ok, chyba rozumiem, dziękuję

4 mar 16:08
3Silnia&6: zad. 4 Niech f(x) = a, a ∊ C
| | 3(x2 −4x + 3) + 13 | | 13 | |
a2 = |
| = 3 + |
| |
| | x2 − 4x + 1 | | x2 − 4x + 1 | |
| | 13 | |
zal. x ∊ C ⇒ x2 − 4x + 1 ∊ C → |
| ≤ 13 → a2 ≤ 16 |
| | x2 − 4x + 1 | |
| | 13 | |
co więcej |
| moze przyjac wartosci 13,−13,1,−1, wiec a = f(x) = −4, −2, −2, 4 |
| | x2 − 4x + 1 | |
Rozwiazujesz kolejno f(x) = −4, −2, −2, 4 i dodatkowo f(x) = 0 − calkowite x to rozwiazanie
4 mar 16:13
Pełcio: Ciekawe rozwiązanie, dziękuję.
A to co napisałem pod tym zadaniem to nie jest prawda?
4 mar 16:19
3Silnia&6: Ty wyznaczyles dziedznine. Wiec to na pewno nie jest prawda

Granica fukcji jest
√3 wiec
wszystkie liczby powiedzmy od milona w gore sa 1< x< 2

nie moga byc calkowite
4 mar 16:23
3Silnia&6: od 10+ chyba juz wystarczy

4 mar 16:24
Pełcio: Rzeczywiście, liczyłem na to, że dziedzina będzie jakaś mała i sprawdzę y dla każdego
całkowitego x z dziedziny, ale nic z tego.
4 mar 16:35
Adamm: x
4+x
2+5=x
4y+2yx
2+y
sprawdzamy ile równanie ma rozwiązań ze względu na parametr y
4 mar 16:45
Adamm: tzn. wystarczy że ma rozwiązania, nie musisz wyznaczać ile ich jest
4 mar 16:48
4 mar 16:49
Adamm: (y−1)x4+(2y−1)x2+y−5=0
jeśli y=1 to x2−4=0 co ma rozwiązania
jeśli y≠1
Δ=(2y−1)2−4(y−1)(y−5)=20y−19≥0
stąd y≥19/20
możemy podstawić y=19/20 i sprawdzić wzorami Viete'a czy faktycznie istnieją wtedy
pierwiastki dodatnie
4 mar 17:02
Pełcio: Dziękuję

4 mar 17:12
Krzysiek: x=tany
| tan2y(tan2y+1)+5 | | tan2ysec2y+5 | |
| = |
| = |
| (tan2y+1)2 | | sec4y | |
=tan
2ysec
2ycos
4y+5cos
4y=sin
2y+5cos
4y=1−cos
2y+5cos
4y=5cos
4y−cos
2y+1=
| | √5 | | 5 | |
(√5cos2y− |
| )+1− |
| |
| | 10 | | 100 | |
| | 95 | | 19 | |
Więc najmniejsza wartość to |
| = |
| |
| | 100 | | 20 | |
4 mar 18:26
Pełcio: Dzięki
Krzysiek, to już trochę trudniejsze, bo nie znam "sec".
Adamm jak masz jeszcze cierpliwość, to wrócę do 1 zadania..

Dlaczego w przedziale √a∊(√2/2;1) mamy 8 rozwiązań? Czegoś nie widzę po prostu

4 mar 19:43
Adamm: bo wtedy okrąg przecina każdy bok w dwóch miejscach
zatem w sumie 2*4=8 rozwiązań
4 mar 19:55
4 mar 20:29
Pełcio: ślepy jestem.... dziękuję, już teraz będę umiał analogiczne rozwiązać
 Krzysiek
Krzysiek chyba że tak..

też fajne rozwiązanie

4 mar 20:36
Pełcio: a2+b2+c2≥ a√bc+b√ac+c√ab
ma ktoś pomysł? a,b,c− nieujemne, czyli pewnie średnie, ale coś mi nie może pyknąć
4 mar 23:15
relaa:
Wykorzystując nierówności między średnimi
| 1 | | 1 | | 1 | | ab + bc + ac | | 1 | | 1 | | 1 | |
| + |
| + |
| = |
| ≥ |
| + |
| + |
| |
| a | | b | | c | | abc | | √ab | | √bc | | √ac | |
ab + bc + ac ≥ c
√ab + a
√bc + b
√ac
a
2 + b
2 + c
2 ≥ ab + bc + ac ≥ c
√ab + a
√bc + b
√ac.
4 mar 23:43
Adamm: (a√bc+b√ac+c√ab)2≤(a2+b2+c2)(ac+bc+ab)
z nierówności Schwarza
również (ac+bc+ab)2≤(a2+b2+c2)2 z nierówności Schwarza
zatem (a√bc+b√ac+c√ab)2≤(a2+b2+c2)2
skąd a√bc+b√ac+c√ab≤a2+b2+c2
4 mar 23:46
Pełcio: Dzięki koledzy

4 mar 23:55
Pełcio: a takie?
23415*(a+b+c+d)≥15*a115*b215*c415*d815
pewnie geometryczna i arytmetyczna, tylko jak?
5 mar 00:32
Adamm: | a+2*b/2+4*c/4+8*d/8 | |
| ≥(ab2*c4*d8)1/15 |
| 15 | |
5 mar 00:37
Adamm: i proszę cię, nie używaj u, jeśli już musisz to pisz nawiasy
5 mar 00:38
Adamm: | | a+2*b/2+4*c/4+8*d/8 | | a*b2*c4*d8 | |
źle, |
| ≥( |
| )1/15 |
| | 15 | | 22*44*88 | |
5 mar 00:40
Pełcio: Teraz by się zgadzało, dzięki.
5 mar 00:54
 Takie zadanka znalazłem:
1. Określ liczbę rozwiązań układu w zależności od parametru a:
Takie zadanka znalazłem:
1. Określ liczbę rozwiązań układu w zależności od parametru a:


 1. graficznie
|y|+|x|=1
|y|=1−|x| dla 1−|x|≥0 czyli 1≥x≥−1
y=1−|x| lub y=|x|−1
dla a>0 mamy
dla √a=1 mamy 4 rozwiązania
dla √a=√2/2 mamy 4 rozwiązania
dla √a∊(√2/2;1) mamy 8 rozwiązań
dla reszty brak
1. graficznie
|y|+|x|=1
|y|=1−|x| dla 1−|x|≥0 czyli 1≥x≥−1
y=1−|x| lub y=|x|−1
dla a>0 mamy
dla √a=1 mamy 4 rozwiązania
dla √a=√2/2 mamy 4 rozwiązania
dla √a∊(√2/2;1) mamy 8 rozwiązań
dla reszty brak

 Racja Silnia, dzięki
Racja Silnia, dzięki 
 x2+y2≤2(|x|+|y|) ⇔ x2−2|y|+y2−2|x|≤0 ⇔
⇔ (|x|−1)2+(|y|−1)2≤2
dla x≥0 oraz y≥0 mamy koło o środku (1;1) i promieniu √2
podobnie dla reszty
otrzymujemy rysunek
wyznaczając pole wycinka zaznaczonego na niebiesko dostajemy pole
x2+y2≤2(|x|+|y|) ⇔ x2−2|y|+y2−2|x|≤0 ⇔
⇔ (|x|−1)2+(|y|−1)2≤2
dla x≥0 oraz y≥0 mamy koło o środku (1;1) i promieniu √2
podobnie dla reszty
otrzymujemy rysunek
wyznaczając pole wycinka zaznaczonego na niebiesko dostajemy pole

 Granica fukcji jest √3 wiec
wszystkie liczby powiedzmy od milona w gore sa 1< x< 2
Granica fukcji jest √3 wiec
wszystkie liczby powiedzmy od milona w gore sa 1< x< 2  nie moga byc calkowite
nie moga byc calkowite


 Dlaczego w przedziale √a∊(√2/2;1) mamy 8 rozwiązań? Czegoś nie widzę po prostu
Dlaczego w przedziale √a∊(√2/2;1) mamy 8 rozwiązań? Czegoś nie widzę po prostu 
 Krzysiek chyba że tak..
Krzysiek chyba że tak..  też fajne rozwiązanie
też fajne rozwiązanie 
