AS:
x
2 − 1 dla −2 < x < −1
|x
2 − 1| = 1 − x
2 dla −1 < x < 1
x
2 − 1 dla 1 < x < 2
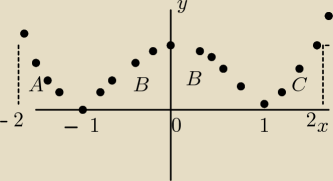
Obszar składa się z trzech części,symetrycznie położonych
A i C obszary równe , wystarczy obliczyć pole obszaru z przedziału <1,2>
oraz dwa obszary B,wystarczy obliczyć pole obszaru z przedziału <0,1>
Obliczam pole obszaru C
2 2
P1 = ∫(x
2 − 1)dx = x
3/3 − x | = (8/3 − 2) − (1/3 −1) = 7/3 − 1 = 4/3
1 1
Z uwagi na symetrię pole obszaru A = 4/3 tyle samo co C
Pole obszaru B
1 1
P1 = ∫(1 − x
2)dx = x − x
3/3 | = (1 − 1/3) − (0/3 − 0) = 2/3
0 0
Pole całego poszukiwanego obszaru
P = A + 2*B + C = 4/3 + 2*2/3 + 4/3 = 4/3 + 4/3 + 4/3 = 12/3 = 4
 x2 − 1 dla −2 < x < −1
|x2 − 1| = 1 − x2 dla −1 < x < 1
x2 − 1 dla 1 < x < 2
Obszar składa się z trzech części,symetrycznie położonych
A i C obszary równe , wystarczy obliczyć pole obszaru z przedziału <1,2>
oraz dwa obszary B,wystarczy obliczyć pole obszaru z przedziału <0,1>
Obliczam pole obszaru C
2 2
P1 = ∫(x2 − 1)dx = x3/3 − x | = (8/3 − 2) − (1/3 −1) = 7/3 − 1 = 4/3
1 1
Z uwagi na symetrię pole obszaru A = 4/3 tyle samo co C
Pole obszaru B
1 1
P1 = ∫(1 − x2)dx = x − x3/3 | = (1 − 1/3) − (0/3 − 0) = 2/3
0 0
Pole całego poszukiwanego obszaru
P = A + 2*B + C = 4/3 + 2*2/3 + 4/3 = 4/3 + 4/3 + 4/3 = 12/3 = 4
x2 − 1 dla −2 < x < −1
|x2 − 1| = 1 − x2 dla −1 < x < 1
x2 − 1 dla 1 < x < 2
Obszar składa się z trzech części,symetrycznie położonych
A i C obszary równe , wystarczy obliczyć pole obszaru z przedziału <1,2>
oraz dwa obszary B,wystarczy obliczyć pole obszaru z przedziału <0,1>
Obliczam pole obszaru C
2 2
P1 = ∫(x2 − 1)dx = x3/3 − x | = (8/3 − 2) − (1/3 −1) = 7/3 − 1 = 4/3
1 1
Z uwagi na symetrię pole obszaru A = 4/3 tyle samo co C
Pole obszaru B
1 1
P1 = ∫(1 − x2)dx = x − x3/3 | = (1 − 1/3) − (0/3 − 0) = 2/3
0 0
Pole całego poszukiwanego obszaru
P = A + 2*B + C = 4/3 + 2*2/3 + 4/3 = 4/3 + 4/3 + 4/3 = 12/3 = 4