analiza pochodna: Witam. Mam problem w analizie funkcji.

	2x3
f(x)=		, dziedzina to R\ {−2,2}
	x2−4

	2x4−24x2
f'(x)=
	(x2−4)2

x²(x²−12)=0 x=0 V x=−√12 V p={12} F rosnaca dla x(−∞;−√12) suma (√12;∞) F malejaca dla x(−√12;√12)\{−2,2}

	16x3+192x
f''(x)=
	(x2−4)3

Miejsca 0 16x(x²+12)=0 x=0 wiec f wypukla dla x(0,2) suma (2;∞) f wklesla dla x(−∞;−2) suma (−2;0) Na wykresie oryginalnej funkcji wychodziloby, ze od (−2;0) funkcja bylaby wypukla i malejaca, natomiast mi z analizy wychodzi, ze dla (−2;0) funkcja bylaby wklesla i malejaca. Wychodziloby,ze robię jakis blad przy odczytaniu przedzialow wkleslosci i wypuklsci. Bardzo prosilbym o wyjasnienie

pochodna: ?

Jerzy: Funkcja jest wypukła w (−2;0) U ( 2;+∞) Funkcja jest wklęsła w (−∞;−2) U (0;2) Punkt przegięcia: x = 0

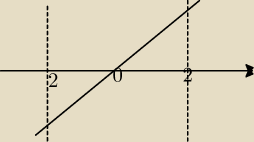
pochodna: moglbys narysowac podgladowy rysunek 2 pochodnej, z ktorej to odczytales ? bo mi wyszlo cos takiego

Jerzy: Tutaj masz wykres tej funkcji: http://www.wolframalpha.com/input/?i=y+%3D+2x%5E3%2F(x%5E2-4)

pochodna: tzn. chodzi mi tylko o odczytaniu wkleslosci i wypuklosci bo tutaj wykonuje blad. czyli musze rysowac zly podgladowy wykres 2 pochodnej 16x(x²+12)=0 i stad mi wynikka taki rysnek jak narysowalem wyzej

Jerzy: Druga pochodna zeruje zeruje się tylko w zerze i tam zmienia znak ( punkt przegięcia)

pochodna: wszystko juz wiem. bardzo dziekuje