trygonometria ape:

	√2
1. Równanie sinx =		ma w przedziale <a, b> dokładnie 4 rozwiązania. Wynika stąd, że:
	2

A. b − a ≥ 2,5π B. b − a ≥ 3π C. b − a ≤ 3,5π D. b − a ≤ 4π Poprawna odpowiedź to A ale nie wiem jak do tego dojść.

	1		√3
2. Funkcję y = −		sinx +		cosx można zapisać w postaci:
	2		2

	π
A. y = sin ( x +		)
	6

	π
B. y = sin ( x +		)
	3

	2π
C. y = sin ( x +		)
	3

	5π
D. y = sin ( x +		)
	6

Odp. C

	√3		π		1
Ze wzoru wychodzi, że sinus ma być równy		czyli		a cosinus −		czyli
	2		3		2

	2π		4π
		lub		co mi się nie zgadza z odpowiedzią.
	3		3

3. Niech P = sin10 + sin20 + sin30 + ... + sin180 oraz Q = cos10 + cos20 + cos30 + ... + cos180. Wynika stąd, że: A. P = 0 B. Q = 0 C. Q = −1 D. P² + Q² = 1 Odp. C.

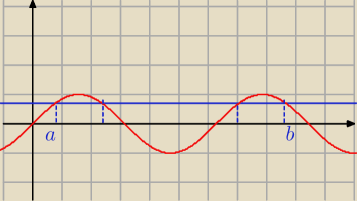Janek191: z.1

	√2
sin x =
	2

	π		3
x =		+ 2π*k lub x =		π +2π*k
	4		4

więc

	π		3		π		3
x1 =		x2 =		π x3 =		+ 2π x4 =		π + 2π
	4		4		4		4

a ≤ x₁ < x₄ ≤ b

	π
a ≤
	4

	3
x4 ≤		π + 2π ≤ b
	4

zatem

	3		π		π
b − a ≥		π + 2π −		= 2π +		π = 2,5 π
	4		4		2

Pytający:

	−π		−1		−π		√3
2. sin(		)=		, cos(		)=
	6		2		6		2

	−π		−π		−π		π
y = sin(		)sinx(x)+cos(		)cos(x) = cos(x−		) = cos(x+		) =
	6		6		6		6

	π		π		2π
=sin(x+		+		) = sin(x+		)
	6		2		3

Pytający: 3. Wszędzie powinny być dopisane stopnie jak mniemam. Q=cos10^o+cos20^o+...+cos80^o+cos90^o+cos100^o+...+cos170^o+cos180^o= =cos10^o+cos20^o+...+cos80^o+cos90^o+cos(180−80)^o+...+cos(180−10)^o+cos180^o= =cos10^o+cos20^o+...+cos80^o+cos90^o+(−cos80^o)+...+(−cos10^o)+cos180^o= =cos90^o+cos180^o = 0−1 = −1

ape: Dziękuję Wam za pomoc.