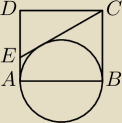
 Na rysunku przedstawiono jest kwadrat ABCD o boku długości 2 oraz okrąg k o średnicy AB.
Punkt E leży na boku AD i odcinek łączący wierzchołek C z punktem E jest styczny do okręgu k.
Oblicz długość odcinka CE.
Proszę o pomoc.
Na rysunku przedstawiono jest kwadrat ABCD o boku długości 2 oraz okrąg k o średnicy AB.
Punkt E leży na boku AD i odcinek łączący wierzchołek C z punktem E jest styczny do okręgu k.
Oblicz długość odcinka CE.
Proszę o pomoc.
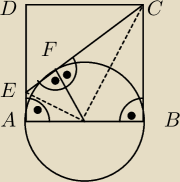 Z podobieństwa trójkątów:
|BC|=|CF|=2
|AE|=|EF|
|CE|=|CF|+|EF|=2+|EF| ⇒ |EF|=|CE|−2
Z ΔCDE:
|CE|2=22+(2−|AE|)2
|CE|2=22+(2−|EF|)2
|CE|2=22+(2−(|CE|−2))2
|CE|2=22+(4−|CE|)2
|CE|2=4+16−8|CE|+|CE|2
Z podobieństwa trójkątów:
|BC|=|CF|=2
|AE|=|EF|
|CE|=|CF|+|EF|=2+|EF| ⇒ |EF|=|CE|−2
Z ΔCDE:
|CE|2=22+(2−|AE|)2
|CE|2=22+(2−|EF|)2
|CE|2=22+(2−(|CE|−2))2
|CE|2=22+(4−|CE|)2
|CE|2=4+16−8|CE|+|CE|2
| 5 | ||
|CE|= | ||
| 2 |