Styczna prostopadła do prostej Maciek: Wyznacz równanie stycznej do wykresu funkcji f(x) = x³ − 3x² + x , która jest prostopadła do prostej x − 2y− 6 = 0 Zamotałem się w rozwiązywaniu i teraz sam nie wiem co robie dobrze a co źle Obliczyłem współczynnik kierunkowy stycznej "−2" Pochodna wyszła mi f'(x) = 3x² −6x + 1 Punkt x₀ (1,−1) równanie stycznej y = −2x + 3 Czy ten wynik jest dobry?

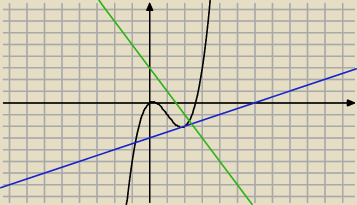
5-latek: To jest Twoja sytuacja (wiec ?

5-latek: Jesli x₀=1 i y₀=−1 to rownanie prostej prostopadlej i przechodzcej przez ten punkt bedzie takie y= a(x−x₀)−y₀ y= −2(x−1)−1 y= −2x+2−1= −2x+1 Treraz sobie sprawdz na wykresie

piotr: równanie stycznej y = −2x + 1

Maciek: Teraz zauważyłem, błąd rachunkowy zrobiłem i to dlatego, dzięki za podpowiedź