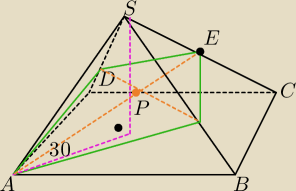
 Na rysunku obok przedstawiono ostrosłup prawidłowy czworokątny o wszystkich krawędziach równej
długości. Oblicz pole przekroju zaznaczonego na rysunku, jeśli płaszczyzna przekroju tworzy z
podstawą kąt 30o.
Próbowałem robić tak z kąta 30, 60, 90. Potem mały trójkąt w deltoidzie jest równoboczny o boku
1/2 a i tyle samo wynosi krótsza przekątna, a dłuższa przekątna to a(√2 + √3/4). I
niestety pole wychodzi błędne.
Punkt E jest środkiem odcinka SC.
Na rysunku obok przedstawiono ostrosłup prawidłowy czworokątny o wszystkich krawędziach równej
długości. Oblicz pole przekroju zaznaczonego na rysunku, jeśli płaszczyzna przekroju tworzy z
podstawą kąt 30o.
Próbowałem robić tak z kąta 30, 60, 90. Potem mały trójkąt w deltoidzie jest równoboczny o boku
1/2 a i tyle samo wynosi krótsza przekątna, a dłuższa przekątna to a(√2 + √3/4). I
niestety pole wychodzi błędne.
Punkt E jest środkiem odcinka SC.
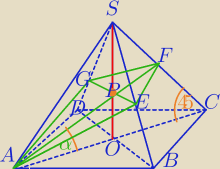 W ΔACF:
α=30o
|AC=a√2
1) Z tw. sinusów:
W ΔACF:
α=30o
|AC=a√2
1) Z tw. sinusów:
| |AC | |AF| | ||
= | |||
| sin(180−(30+45)) | sin45 |
| a | ||
|AF|= | ||
| sin75 |
| a√2 | ||
|OS|= | ||
| 2 |
| |OP| | ||
tgα= | ||
| |AO| |
| √3 | |OP| | a√6 | |||
= | ⇔|OP|= | ||||
| 3 | 0.5a√2 | 6 |
| a√2 | a√6 | a*(3√2−√6 | ||||
|PS|= | − | = | ||||
| 2 | 6 | 6 |
| a | a*(3√2−√6 | |||
PAEFG=|AF|*|PE|= | * | |||
| sin75 | 6 |
| 4 | a*(3√2−√6 | |||
PAEFG=a2* | * | = | ||
| (√6+√2) | 6 |
| 2(√6−√2)*(3√2−√6) | ||
=a2* | ||
| 3*(6−2) |
| a2*(4√3−6) | ||
PAEFG= | ||
| 3 |
