całka Krzysiek: Jak chce na przykład obliczyć pole koła za pomocą całki to skąd mam wiedzieć jakie są granice całkowania? I że jak jest na przykład od 0 do r to trzeba jeszcze pomnożyć razy 4?

Jerzy: Najlepiej przejść na współrzędne biegunowe.

Krzysiek: A co to?

Alky: Czemu akurat razy 4 ?

Krzysiek: Bo wtedy liczymy tylko jedną cwiartkę koła więc trzeba pomnożyć razy 4 aby policzyć pole całego

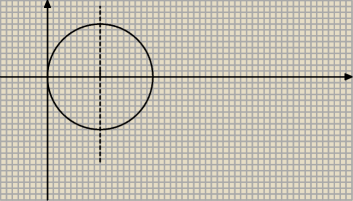
Alky: No wiem wiem. Zawsze możesz dać się oszaleć i zapisać inną funkcję ograniczającą z dołu i pomnożyć razy 2, ale to trochę szalone Jeśli chodzi o granice całkowania to w takim przypadku w sumie mozesz sobie dobrać jak Ci wygodniej. Możesz tak jak mówisz liczyć od 0 do r , od zera do 2r i w zaleności od tego jak dobierzesz funkcje ograniczające mnożysz razy ilość ćwiartek. Nikt nie narzuca sposobu

'Leszek: Panowie ,przeciez rownanie okregu np. x² + y² = 4 nie jest funkcja , natomiast y = √4 − x² dla x= < − 2 , 2 > jest to funkcja i dlatego calka liczona jest dla funkcji i w tym przypadku nalezy wynik pomnozyc przez 2 . Ale najlepiej liczyc takie calki uzywajac tak jak napisal to p.Jerzy wspolrzednych biegunowych .

Jack: Krzysiek Spojrz na to.z tej strony − zawsze obliczasz czesc ponad nad osia OX. Dlagego jesli narysujemy okrag np onsrodku w punkcie P(0,4) i promieniu 2 to owszem jesli liczymy calke od 0 do r to.dostaniemy cwiartke kola wiec muaimy ja pomnozyc razy 4. Z kolei jesli zrobimy rysunek jak Alky no to liczac calke od 0 do 2r uzyskamy polowe kola

Alky: Leszek wlasnie mialem na mysli żeby wziąć nie równanie okregu tylko funkcje ograniczajaca od góry jako górną część z tego okregu i od dołu ograniczającą funkcje przeciwna do tej ograniczajacej od góry. A co do współrzednych biegunowych to mówił, że nie miał jeszcze więc nie ma co wciskać..

Kora: A nie lepiej zrobic, ze skoro x²+y²=r² to policzyc sobie x=rcosδ i y=rsinδ

Jerzy: Napisałem już to wczoraj 23:22.

Kora: Ahh ok fakt, moj blad

Alky: A zaraz potem autor napisał że jeszcze nie miał w ogóle do czynienia ze wsp.biegunowymi. Jasne, że łatwiej, ale poki co raczej noe tedy droga. Może ktos jeszcze zaproponuje ten sposób, bo mało tu tego było ?

'Leszek: Obliczenie pola polkola za pomoca calki pojedynczej jest klopotliwe Np. f(x) = √4 − x² dla x= < − 2 , 2 > P = 2 ∫ √ 4 − x² dx w granicach x =< − 2 , 2 > Nie jest to calka elementarna i trzeba wykonac podstawienie np x/2 = sin t i nastepnie calkujemy przez czesci ?

Jerzy:

	1 + cos2t
Niekoniecznie przez części ... dostaniemy całkę: 4∫cos2dt = 4∫		dt
	2

w granicach: [−π/2;π2]

'Leszek: OK! Jerzy racja zapomnialem o takiej tozsamosci trygonometrycznej .