Geometria analityczna
Kacperek: Dane są punkty A = (1,2) B = (4,3) na prostej y=4 wyznacz punkt C tak,
aby łamana A⊂B miała najmniejsza długość.
2 mar 21:08
5-latek: ⊂ to jest symbol zawierania sie
jesli A zawiera sie w B to lamana to bedzie prosta
2 mar 21:13
Janek191:
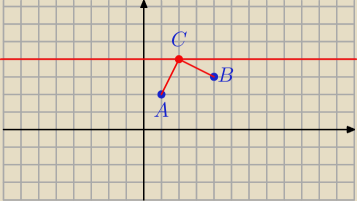
C = ( x, 4)
więc
L(x) =
√( x − 1)2 + ( 4 − 2)2 +
√( 4 − x)2 + ( 3 − 4)2
L(x) =
√ (x −1)2 + 4 +
√(4 − x)2 + 1
itd.
2 mar 21:14
Ola1987 : Czy przy punkcie C będzie kąt prosty?
2 mar 21:17
Mila:
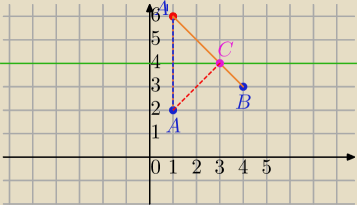
A = (1,2) B = (4,3)
1) Wyznaczyć punkt symetryczny do A względem prostej y=4
A=(1,2), A'=(1,6)
2) łączymy punkty A' i B
Punkt przecięcia z prostą to szukany punkt
C=(3,4)
Algebraicznie:
Prosta A'B:
y=ax+b
6=a+b i 3=4a+b
stąd:
a=−1 i b=7
y=−x+7
y=4
−x+7=4 stąd x=3 i
C=(3,4)
=======
2 mar 21:36
 C = ( x, 4)
więc
L(x) = √( x − 1)2 + ( 4 − 2)2 + √( 4 − x)2 + ( 3 − 4)2
L(x) = √ (x −1)2 + 4 + √(4 − x)2 + 1
itd.
C = ( x, 4)
więc
L(x) = √( x − 1)2 + ( 4 − 2)2 + √( 4 − x)2 + ( 3 − 4)2
L(x) = √ (x −1)2 + 4 + √(4 − x)2 + 1
itd.
 A = (1,2) B = (4,3)
1) Wyznaczyć punkt symetryczny do A względem prostej y=4
A=(1,2), A'=(1,6)
2) łączymy punkty A' i B
Punkt przecięcia z prostą to szukany punkt
C=(3,4)
Algebraicznie:
Prosta A'B:
y=ax+b
6=a+b i 3=4a+b
stąd:
a=−1 i b=7
y=−x+7
y=4
−x+7=4 stąd x=3 i
C=(3,4)
=======
A = (1,2) B = (4,3)
1) Wyznaczyć punkt symetryczny do A względem prostej y=4
A=(1,2), A'=(1,6)
2) łączymy punkty A' i B
Punkt przecięcia z prostą to szukany punkt
C=(3,4)
Algebraicznie:
Prosta A'B:
y=ax+b
6=a+b i 3=4a+b
stąd:
a=−1 i b=7
y=−x+7
y=4
−x+7=4 stąd x=3 i
C=(3,4)
=======