Hmmm troszkę opisu z rysowaniem trójkąta? cynamonek: Punkty A=(2,−1) i B=(−6,3) są końcami przeciwprostokątnej równoramiennego trójkąta prostokątnego ABC. Wyznacz współrzędne wierzcołka C i oblicz dlugość promienia okręgu wpisanego w ten trójkąt.

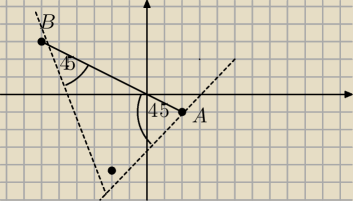
5-latek: Ja bym to zrobil tak Skoro AB to przecowprostokatna to napisalbym roznie prostej przecinajacej os OX Pod katem 45^o i przechodzacej prze punkt A ROwniez napiaslbym rownanie prostej przecinajacej os OX pd katem 135^o i przechodzacej prze punkt B Wyliczyl punkt C przeciecia prostych Obliczyl dlugosci przyprostkatnej i przecowprostokatnej

	a+b−c
r=
	2

tg45^o=1 tg135^o=−1

5-latek: To jest tylko szkic do zadania (ten rysunek

5-latek: Wiesz teraz tak patrze i chyba zle cos jest

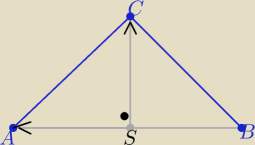Eta: → AS= [−4,2] i wektory AS i CS są prostopadłe i równej długości → CS =[x+2, y−1] z warunku prostopadłości CS=[2, 4] lub [−2, −4] to x+2=2 i y−1=4 lub x+2= −2 i y−1=−4 .................. C₁(0,5) lub C₂( −4,−3) teraz już sam dokończ drugą część zadania

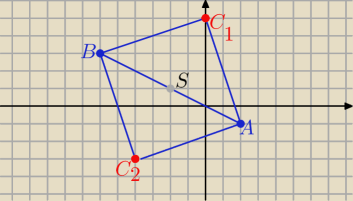Eta: Jest ok ... co można dopiero teraz sprawdzić w układzie współrzędnych

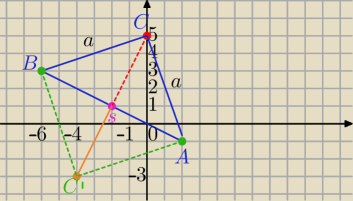Mila: Punkty A=(2,−1) i B=(−6,3) AB− przeciwprostokątna S− środek przeciwprostokątnej

	2−6		−1+3
S=(		,		)=(−2,1)
	2		2

|SC|=|SA| i SC^→⊥SA^→ SA^→=[4,−2] SC^→=[2,4] lub SC'→=[−2−4] S=(−2,1)→T{[2,4]|→C=(−2+2,1+4)⇔C=(0,5) lub (−2,1)→T_{[−2,−4]|→C=(−2−2,1−4)⇔C'=(−4,−3) 2) Promień okręgu wpisanego w ΔABC: a=√2²+6²=√40=2√10 c=√8²+4²=√80=4√5

	1
PΔ=		*2√10*2√10=20
	2

	2√10+2√10+4√5
PΔ=		*r
	2

(2√10+2√5)*r=20 (√10+√5)*r=10 /*(√10−√5) (10−5)*r=10*(√10−√5) r=2(√10−√5) ===========

5-latek: jasne ze jest zle Musimy napisac rownaie prostej przechodzacej prze punkt A pod katem 45^o do prostej AB Poszukiwana prosta ma wspolczynnik kierunkowy m

	3+1		1
Prosta AB ma wspolczynnik kierunkowy m1=		= −
	−6−2		2

Ze wzoru na tangens miedzy prostymi mamy

	|m−m1|
tgφ=
	m*m1+1

wyliczymy m φ= 45^o to tgφ= 1

1   |m+ |   2
	=1
1   − m+1   2

	1		1
|m+		|= −		m+1
	2		2

wylicz z tego m

	1		1
m+		= −		m+1
	2		2

3		1
	m=
2		2

	1
m=
	3

	1		1
−m−		= −		m+1
	2		2

m=−3 Dostaniesz dwa rownania potem piszsez rownania prostych prostopadlych do nich przechodzacych prze B i masz rownania przyprostokatnych Punkt przeciecia tych prostych to punkt C Teraz powinno byc dobrze

5-latek: Dobry wieczor Paniom

Eta:

	1
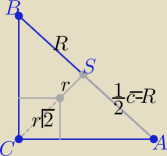
Można r obliczyć też tak |CS|=R=		|AB|
	2

	1
|CS|=r+r√2 ⇒r+r√2=R=		c
	2

w zadaniu |AB|= c=4√5 to r(√2+1)=2√5 /*(√2−1) ⇒r= 2√5(√2−1)