Zbadaj przebieg funkcji e^x/pierwiastek z x Santi:

	ex
Zbadaj przebieg funkcji
	√x

Byłbym naprawdę bardzo wdzięczny za pomoc, łatwiejsze przykłady jestem zrobić, ale taki jak ten tutaj to dla mnie czarna magia

Jack: Przejdzmy przez to razem. 1. Dziedzina funkcji 2. Miejsca przeciec z osami. Reszta za chwile.

Santi: 1. Df = (0:∞) 2. Nie przecina osi OX, OY także nie, może tylko dążyć do 0, ale tego podpunktu już pewien nie jestem

Jack: Ok. 3. Granice (do asymptot) Skoro funkcja ma dziedzine (0;∞) To jedyne granice jaki jest sens badac to lim. f(x) x−>0⁺ oraz lim f(x) x−>∞ 4. Pochodna i jej dziedzina.

Santi: 3. lim. f(x) x−>0+ → ∞ zrobiłem metodą tabelki, ale podstawiłem 4,2 i 1, ponieważ na kalkulatorze prostym nie bardzo da się wymyślić coś innego, ale nie wiem, czy takie duże liczby zostałyby uznane ? lim f(x) x−>∞ → ∞

	ex(√x−1)
4. Doszedłem do postaci f'(x) =		i... nie mam pojęcia jak to dalej
	2√x*x

rozbić, wiem, że w mianowniku powinienem chyba zostawić kwadrat, natomiast dziedzina pozostanie taka sama

Jack: 1) dlaczego tabelka?

	ex		e0		1
lim.		=		=		= ∞
	√x		√0		0+

x−>0⁺ Mozna by powiedziec ze sa 2 takie intuicyjne wzory

	liczba dodatnia		liczba ujemna
granica		= ∞ oraz		= − ∞
	0+		0+

Oczywiscie jakby bylo na dole 0⁻ to jesli u gory oiczba ujemna to wychodzimy na ∞ bo minusy sie ze tak powiem skroca. A teraz wniosek z tego. Skoro nasza granica wynosi nieskonczonosc, to znaczy ze jest tu asymptota. Co wiecej badalismy to dla konkretnego iksa (jakiejs liczby − tutaj zera) a nie badalismy w nieskonczonosciach zatem jest to granica pionowa No i na koniec jakp ze badalismy przy 0⁺ to jest to granica prawostronna. Zatem.mamy x=0 granica pionowa prawostronna. Teraz ta druga granica przy x−>∞ wyszla ∞ czyli w tym wypadku skoro badalismy granice w nieskonczonosci to badalismy istnienie asymptot poziomych. Nie wyszla nam.zadna konkretna liczba (bo wyszla nieskonczonosc), wiec wniosek: brak asymptot poziomych. Co do pochodnej to za chwilke, bo herbatka

Santi: Dziękuję bardzo za wytłumaczenie bliżej asymptot i granic, szkoda, że podręczniki akademickie nie są pisane w tak przyjazny sposób

Jack: ok, zatem faktycznie dziedzina bedzie ta sama, ale warto mimo wszystko napisac D_f' = (0;∞) natomiast sama pochodna

	f(x)		f'(x) * g(x) − g'(x) * f(x)
(korzystamy ze wzoru : pochodna z		=		)
	g(x)		[g(x)]2

zatem

	1   ex(√x) − * ex   2√x		1   ex(√x − )   2√x
f'(x) =		=		=
	(√x)2		x

	√x * 2√x − 1   ex( )   2√x		2x−1   ex( )   2√x		ex(2x−1)
=		=		=
	x		x		2√x * x

No i teraz 5. przyrownujemy pochodna do zera 6. rysujemy krzywa,aby moc okreslic monotonicznosc i ekstrema

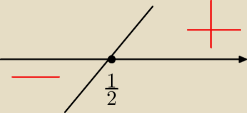
Jack: tak powinien wygladac wykres pochodnej

Santi: Ogromnie dziękuję za całą pomoc, dzięki Panu pojawił się przede mną cień szansy na zdanie kolokwium

Jack: żadne "panu" dokonczy my/sz ?

Santi:

	ex(2x−1)		1
5.		=0 ⇔ 2x−1=0 x=
	2√x * x		2

6. Za chwilę postaram się narysować

Jack: 5. 6. krzywa powinna wygladac dokladnie tak jak ja narysowalem 19:10 Odczytujemy monotonicznosc i ekstrema, zatem jesli chodzi o monotonicznosc, to najlepiej jakby to byl mniej wiecej taki zapis dla x ∊ (tu podajemy przedzial) f ' (x) (> 0 lub < 0) funkcja (rosnie/maleje) przyklad niezwiazany z zadaniem : dla x ∊ <2;3> f ' (x) > 0 funkcja rosnie (lub po prostu f ↗)

Jack: dobra, dokoncze, (bo to nie koniec)

	1
dla x ∊ (−∞;		> f ' (x) < 0 funkcja maleje
	2

	1
dla x ∊ <		;∞) f ' (x) > 0 funkcja rosnie
	2

	1
dla x =		mamy ekstremum lokalne minimum
	2

(dlaczego minimum, najpierw mamy funkcje ponizej zera, wiec mozna sobie wyobrazic ze idziemy w dol, a potem powyzej czyli szlismy w dol, a teraz idziemy w gore, wiec skoro na poczatku w dol,a potem w gore, no to w pewnym punkcie musielismy byc najnizej, dlatego minimum)

	1		e1/2		√e
f(		) =		=		= √e * √2 = √2e
	2		√1/2		1   √2

	1
zatem, dla x =		mamy ekstremum lokalne minimum, ktorego wartosc wynosi √2e.
	2

liczymy pochodna drugiego rzedu, czyli pochodna z tej pochodnej co juz policzylismy

	ex(2x−1)		ex(4x2−4x+3)
f''(x) = (		)' = ... =
	2√x*x		4*x2*√x

dla f''(x) > 0 funkcja jest wypukla

	ex(4x2−4x+3)
		> 0 /:ex (bo na pewno jest nieujemne)
	4*x2*√x

4x2−4x+3
	> 0 /*4x2√x (na pewno nie jest ujemne, wiec nie zmieniam znaku)
4x2√x

4x²−4x+3 > 0 ... dla f''(x) < 0 funkcja jest wklesla, czyli dla ... 4x² − 4x + 3 < 0 ... I teraz nalezy stworzyc tabelke, zawrzec w niej wszystkie informacje, i sprobowac narysowac wykres