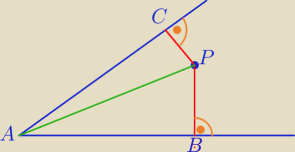
Dany jest kąt ostry o wierzchołku A i punkt P należący do wnętrza tego kąta. Ania: Dany jest kąt ostry o wierzchołku A i punkt P należący do wnętrza tego kąta. Niech PB i PC ozn odległości punktu P do ramion kąta i niech PB>PC. Wówczas a. promień okregu opisanego na ΔABP jest większy od promienia kręgu opisaneg na ΔACP b. AP²=PB²+PC² c. w czworokąt ABPC można wpisać okrąg d. na czworokącie ABPC można opisać okrąg Odpowiedz uzasadnij

Mila:

	1
a) nieprawda, Δ są prostokątne o wspólnej przeciwprostokątnej R=		|AP| dla obu
	2

trójkątów. b) nie c) nie d) tak, Sumy kątów : ∡B+∡C=180^o⇔∡A+∡P=180⇔na czworokącie ABPC można opisać okrąg