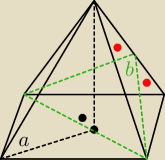
Stereometria Michał: W ostrosłupie prawidłowym czworokątnym kąt nachylenia krawędzi do podstawy jest równy α. Wykaż, że:

	−1
cos β =
	1 + 2 tg2α

gdzie β jest kątem między sąsiednimi ścianami bocznymi. Wyliczam, że: k − krawędź boczna

	a√2
cos α =		* k
	2

2 cos α = a√2 * k k = ^{2 cos α}_a√2 Następnie wysokość ściany bocznej to: h² + 1/2 a² = k² I tutaj już przestaje mi trochę wychodzić. Proszę o pomoc.

Jerzy:

	x
Masz błąd: cosα =		, gdzie: x to połowa przekatnej podstawy.
	k

Michał: Oznaczyłem a jako krawędź podstawy, więc x = a√2 / 2. Czy lepiej to zapisywać jako x po prostu?

Jerzy:

	a√2   2
Popatrz: cosα =		, a u Ciebie jest źle.
	k

Michał:

	x
Faktycznie. Więc k =
	2 cos α

Następnie mam liczyć wysokość ściany bocznej?

Jerzy:

	a√2
k =
	2cosα

licz wysokość ściany bocznej.

Michał: h² = a²(2 − cos²α) / 4cos²α

Jerzy: OK. Teraz musisz policzyć pole ściany bocznej.

Michał: Trochę ciężko, bo mam tylko wysokość do kwadratu. Czy mogę zastosować zależności: k − krawędź boczna t − wysokość opuszczona na ścianę boczną a − podstawa h − wysokość 1/2 ah = 1/2 kt ah = kt I z tego t² = 2a² − a² cos²α ?

Jerzy:

	a
h =		*√2 − cos2α
	2cosα

teraz będzie łatwiej.

Michał:

	a2
P =		* √2 − cos2 α
	4 cos α

Jerzy: OK. Teraz musisz obliczyć wysokość ściany bocznej opuszczonej na krawdędź k.

Michał: t² = 2a² − a² cos²α t² = a²(2 − cos²) t = a√2 − cos²α

Jerzy:

	1
Nie tak ... P (obliczone) =		*k*H ( H szukana wysokość )
	2

Michał: I teraz twierdzenie cosinusów dla kąta o bokach t, t, a√2/2 ?

Michał:

	a√4 − 2cos α
H =
	2

Jerzy:

	2−cos2α
H = a*√
	2

Michał: I z tego już będę w stanie wyliczyć cos β?

Jerzy: Tak ... albo tw. cosinusów, albo cos(β/2)

Michał: Dziękuję za pomoc.