Całka potrójna Boguś: Mam do policzenia całkę ∫∫∫ √x² + y²dxdydz, opisaną stożkiem x² + y² = x², ograniczoną płaszczyznami z=0 i z=1 Zamieniam na wsp. walcowe. Obszar V: z∊<0,1> φ∊<0,2π> r∊<0,√z² + 1 <−−− dobrze?

Boguś:

'Leszek: Rownanie stozka to : x² + y² = z² Obszar calkowania D : x² + y² = 1 Wspolrzedne biegunowe r = < 0 , 1 > ; φ = < 0 , 2π > ∫ ∫ ∫ √x² + y² dz dx dy = ∫ ∫ r *r dr dφ = 2π * r³/3 = 2π/3

Boguś: Według odpowiedzi ma wyjść π/6 Wcześniej też liczyłem dla r od 0 do 1 i wyszło mi tak samo

Adamm: √x²+y²≤z≤1 ∫∫∫r²dzdrdθ=∫∫r²−r³ drdθ = ∫ 1/12 dθ = π/6 hmmm... mi wyszło

Boguś: A dlaczego tak się dzieje?

Adamm: magia niech ci wytłumaczy 'Leszek, on był pierwszy

Boguś: No ale wychodzi na to, że podał zły wynik?

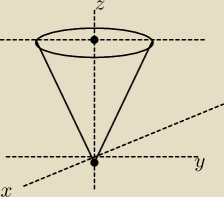
'Leszek: SORRY ,za szybko napisalem i pominalem calke dz ,Adamm podal prawidlowe rozwiazanie ,rysunek tez jest dobry .

Boguś: Okej, tylko nie wiem skąd bierze się to ograniczenie dla z

piotr: granicami całkowania są: powierzchnia boczna stożka x² + y² = z² ⇒ z = √x²+y² = r płaszczyzna z=1

piotr: ∫₀^2π [ ∫₀¹ r² [ ∫_r¹dz ] dr ] dθ

'Leszek: @Bogus , na swoim rysunku dorysuj linie pionowa od powierzchni stozka do plaszczyzny z = 1 i to sa granice calkowania po zmiennej z . Wowczas otrzymasz ∫ ∫ (r² − r³ ) dr dφ