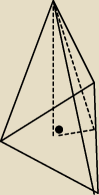
Objętość i pole całkowite ostrosłupa prawidłowego Michał: W ostrosłupie prawidłowym trójkątnym ściany boczne nachylone są do podstawy pod kątem α. Wysokość ścian bocznych jest równa h. Wyznacz objętość i pole powierzchni całkowitej tego ostrosłupa. Zaznaczony trójkąt ma w podstawie 1/3 wysokości trójkąta równobocznego i tylko tyle jestem w stanie ustalić. Nie wiem co dalej. Odp: V = √3h³ sin α cos²α P_c = 3√3h² cos α(1 + cos α)

Jerzy:

	a√3
Musisz obliczyć krawędż podstawy ze wzoru: h =
	2

Jerzy: Kolizja oznaczeń ... h małe w tym wzorze oznacza wysokość podstawy bryły.

	a√3
Oznacz ją np x , wtedy a obliczasz ze wzoru: x =
	2

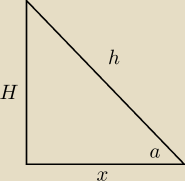
Michał: Tylko co dalej? Mam niewiadomą h, H, 1/3 wysokości podstawy oraz kąt alfa. Nie wiem w jaki sposób zapisać dalsze zależności.

Jerzy: h traktujesz jako znane ( z treści zadania) Najpierw policz x ( to bedzie wg Twojego rysunku 1/3 wysokości podstawy d) ,

	a√3
potem a ( d =		) , a na koncu H.
	2

Jerzy:

	1   d 3
Pierwsza zależność:		= cosα → oblicz: d.
	h

Michał: 3 cos α * h = d

	H
sin α =
	h

sin α = H * ^{3 cos α}_d Tak to trzeba zrobić?

Michał: tg α = sin α / 3 cos α Teraz już sam nie wiem co robię...

Jerzy: Powoli .... mamy: d = 3hcosα teraz oblicz krawędź podstaw: a

Michał: a = ^2√3d₃

Jerzy: Podstaw obliczone wcześniej d.

Michał: Pp = 3√3 * cos²α * h² ?

Jerzy:

	H
Dobrze ... teraz policz wysokość H (		= sinα )
	h

Michał: H = sin α * h Przy czym h = d / 3 cos α I z tego już mogę wyliczyć V?

Jerzy: Do objętości już masz wszystko:

	1
V =		Pp*H .... i licz.
	3

Jerzy: h traktujesz jako wartość znaną !

Michał: Udało się. V = √3h³ * sin α cos²α Bardzo dziękuję za pomoc. Spróbuję jeszcze pole powierzchni całkowitej.

Michał: P_c = P_p + 3P (pola ścian) P_c = a * d + 3 * a * h P_c = a(d + 3h) P_c = 2√3d / 3 (3cos α + 3h) P_c = 2√3d(cos α + h) P_c = 2√3 * 3 cos α * h * h (cos α + 1) P_c = 6√3h² cos α(cos α + 1) W odpowiedziach jest P_c = 3√3h² cos α(cos α + 1) Czy błąd wynika z obliczeń tutaj czy z wcześniej obliczonych danych?

Jerzy: Źle policzyłeś:

	1
Pc = Pp + 3*Ps = 3√3cos2α*h2 + 3*		*2√3cosα*h2 =
	2

= 3√3cos²αh² + 3√3cosα*h = 3√3h²cosα(cosα + 1)

Jerzy: w ostatniej linijce drugi składnik ma być: 3√3cosα*h²

Jerzy: P_p miałeś już policzone: P_p = 3√3cos²α*h²

	1		1
Ps =		a*h =		2√3cosα*h*h = √3cosα*h2
	2		2

Michał: Faktycznie. Policzyłem pole boków jako a * h, zamiast 1/3 * a * h. Zapomniałem że to są trójkąty, a nie prostokąty. Dziękuję jeszcze raz za pomoc.