Planimetria dosix: 3. W trójkącie równoramiennym ABC o podstawie AB, gdzie |AB| = a oraz |AC| = |BC| = b,

	√2x2+b2
poprowadzono środkową AD długości x. Wykaż, że x =
	2

dosix: błąd pod pierwsiatkiem powinno byc 2a²+b²

dosix: pomoze ktos?

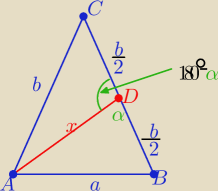Eta: Dwa razy z twierdzenia kosinusów w trójkątach ABD i ADC a²=x²+(b²/4)−2x*(b/2)*cosα i b²=x²+(b²/4)+2x*(b/2)*cosα bo cos(180^o−α)= − cosα + −−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

	√2a2+b2
a2+b2= 2x2+(b2/2) ⇒ 4x2= 2a2+b2 ⇒ x=
	2