Funkcja homograficzna Na sprawdzian Sylar: Zadanie z funkcji homograficzna − tez do sprawdzianu− prosze o pomoc

	ax+b
Dziedzina funkcji f(x)=		jest zbior R\{−1}. Miejscem zerowym funkcji f jest liczba
	x+c

(−1,5) a do jej wykresu nalezy punkt A (−0,5 , −8) a) Oblicz a,b,c b) Narysuj wykres f

	ax+b
c) zbadaj liczbe rozwiazan rownania |		|=m ze wzgledu na wartosc parametru m, m∊ R
	x+c

paziówna: hm jest błąd. miejsce zerowe to miejsce i wyraża się w sposób "x = .." albo "liczba jakaś jest miejscem zerowym" a Ty podałeś/aś punkt... w dodatku, który nie leży na osi OX...

Sylar: dobrze jest przepisane z podrecznika Sprawdzialem dokladnie

paziówna: ale... miejsce zerowe funkcji to takie, w którym funkcja przecina oś OX! Więc dziwną masz książkę...

justka: miejscem zerowym jest liczba:−1.5

Sylar: Zadanie *4.89 /95 Matematyka zbior zadaan do liceow i technikow klasa II zakres podsawowy i roszezony (nowe opracowanie) Krzysztof Klaczkow (taka czarno czerwnona) − dobra nie wazne dalem inne zadanie moze je dasz rade

justka: D = R\{−1}⇒c = 1 f(−1,5) = 0 i f(−0,5) = −8 0 = (−1,5a+b)/(−0,5) −8 = (−0,5a+b)/(0,5) rozwiąż układ równań a= −4 i b =−6 f(x) = (−4x−6)/(x+1)

beata: Też próbuję robić to zadanie więc podłączam się do prośby Sylara

Bogdan:

	3
Zadanie jest poprawnie przez Sylara podane. Miejscem zerowym jest x = −		.
	2

paziówna: ach, no to wszystko jasne!

justka: Aby narysować wykres funkcji f należy sprowadzić go do postaci kanonicznej f(x) = ^{−4(x+1)−2}_x+1 f(x) = ⁻²_x+1 −4 − postać kanoniczna y = ^{− 2}_x wektor [−1; −4] ⇒y = f(x)

kasiek: Rozwiąż równania z parametrem a, (a należy do R)

2x−1		2x		ax−2
	+		=
x−a		a		a2−ax

beata: a część c) zadania Sylara Wie ktoś?

Julek: Z dziedziny c = 1

	3a   − + b   2
0 =		po uporządkowaniu 2b = 3a
	1   −   2

	−a   3a   + 2   2
−8 =		⇒ −4 = a ⇒ b = −6
	1   2

	−4x−6		−4(x+1)−2		−2
f(x) =		=		=		− 4
	x+1		x+1		x+1

	−2
g(x) =		po przesunięciu o wektor v = [−1;−4] otrzymujemy f(x)
	x

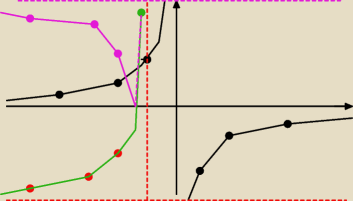
Przyjmijmy, że pozioma, czerwona do y=−4, a fioletowa to y= 4 0 rozwiązań dla m∊(−∞;0) 1 rozwiązanie dla m∊ {0;4} 2 rozwiązania dla m∊ (0;4) ∪ (4;+∞)

−2
	− czerń
x

f(x) − zieleń |f(x)| −

Julek: |f(x)| − fiolet

beata: Może ktoś jeszcze nie śpi? Pomóżcie

beata: Wieeelkie dzięki Julku! Biorę się za analizę Twojego rozwiązania

paziówna:

	−2
f(x) =		− 4
	x+1

	−2
dla		asymptota pozioma y = 0
	x+1

	−2
dla		− 4 asymptota pozioma y = −4
	x+1

brak rozwiązań dla m = −4 dla całej reszty, m∊ℛ\{−4} jedno rozwiązanie

paziówna: ach, wartość bezwględna! najmocniej przepraszam,

Julek: Nie ma problemu Beatko, oczywiście dla Twojej wygody pobazgroliłem, ale nie sugeruj się tak mocno tym rysunkiem bo nie starczyło mi miejsca na dwa ramiona funkcji (jedno powinno być pod czerwoną w prawej ćwiartce, a drugie nad fioletową w prawej)

beata: A czemu fragment wykresu z IV ćwiartki układu nie został przekształcony (przesunięty o wektor [−1, −4] oraz odbity wzgl. OX

beata: Aha Już wszystko jasne ! SUPER Dzięki serdeczne

wieża: Dany jest równoległobok o bokach dł. 10cm , 9cm. jedna z przekątnych dzieli równoległobok na dwa trójkąty prostokątne . oblicz wartość funkcji trygonometrycznych kątów ostrych tych trójkątów.

mery234: Dana jest funkcja określona wzorem f(X)=2/x, x należy do R/(0). Narysuj wykres tej funkcji i podaj zbiór wartości funkcji f. Oblicz argument dla którego funkcja f osiąga wartość (0,4) oraz rozwiąż równanie f(x+3)=f(2x−1). Proszę o pomoc! Dziękuję