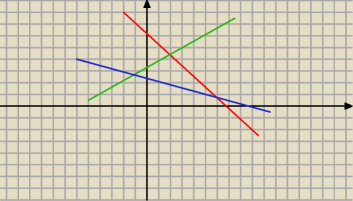
Całkowanie po dwóch obszarach zef: Jak obliczyć przykładowo pole trójkąta za pomocą całki ? Po jednym obszarze wiem jak się to robi np. jak mamy parabolę i prostą ale jak to zrobić w takim trójkącie ?

Jerzy: Podzielic na dwa trojkaty.

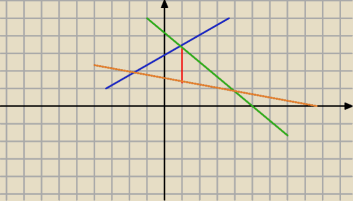
zef: Czerwona kreska to linia dzieląca. n−niebieski z−zielony p−pomarańczowy Wzory tych funkcji. ∫_a^b(n−p)dx+∫_c^d(z−p)dx Tak można ?

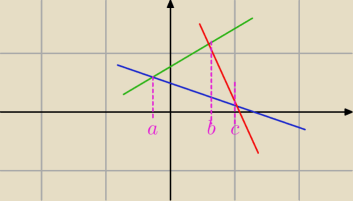
Pytający: P=∫_a^b (f(x)−f(x))dx + ∫_b^c (f(x)−f(x))dx

zef: Pytający, dziękuję ślicznie ! Tak właśnie myślałem, macie panowie może zadanie żeby sprawdzić czy na pewno to umiem ?

Jerzy: Naszkicuj trojkat ktorego pole obliczysz bez calki a potem policz go calką.

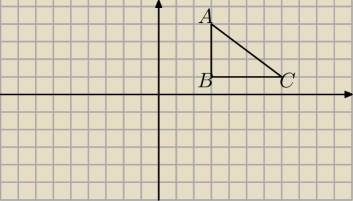
zef: I.P_Δ=0.5*4*3=6 II. y_BC=1 x_AB=3 y_AC=? wyznaczam y_AC gdzie A=(3,4),C=(7,1) 4=3a+b ⇔ b=4−3a

	3		25
1=7a+b .. 1=7a+4−3a .. 4a=−3 a=−0,75 .. b=4−3(−		)=
	4		4

	25
yAC=−0,75x+
	4

x_AB=3 y_BC=1

	25
∫(−0,75x+		−1)dx hmm i tu jest tylko 1 punkt przecięcia więc nie za bardzo wiem jak
	4

wyznaczyć granice całkowania

Jerzy: [3;7]

zef: No ale punkt x=3 jest miejscem przecięcia prostej ac z ab a 7 prostej ac z bc Więc jak to dać do jednej całki ?

Jerzy: x zmienia sie w tych granicach.

Jerzy: Dolna granica x = 3, gorna x = 7

zef: ∫₃⁷y_ac−y_bcdx+∫⁴₁x_ab−x_acdy Myślałem to zrobić w taki sposób, dobrze myślę ?

Jerzy: Tak jak napissles na poczatku i calkuj wcgranicach 3,7

zef:

	25		4		21		3x2		21
∫37(−0,75x+		−		)dx=∫37(−0,75x+		)dx=|−		+		x|37=
	4		4		4		8		4

	−147		147		27		63		147		27		126
[		+		]−[−		+		]=		−[−		+		]=
	8		4		8		4		8		8		8

147		99
	−		=6
8		8

No i zgadza się Dobrze by było jakbym jeszcze z jakimś innym przykładem spróbował

Jerzy: f(x) = √x g(x) = −x + 2

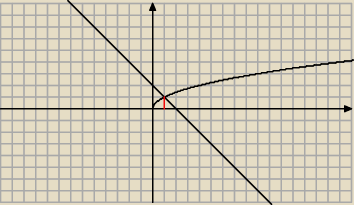
zef: y1=y2 √x=−x+2 //² x=4−4x+x² x²−5x+4=0 Δ=25−16=9

	5−3
x1=		=1
	2

	5+3
x2=		=4
	2

√1=−1+2 1=1, L=P √4=−4+2 2≠−2 L≠P

	2x3/2		−x2
∫01√xdx+∫12(−x+2)dx=|		|01+|		+2x|12=
	3		2

23/2		−1		23/2		1		4√2+2
	+[2−(		+2)]=		+		=		=√2+0.5 Zrobiłem to na 2
3		2		3		2		4

całki bo wydaje mi się że na jednej nie można, chyba żeby całkować po zmiennej y.

zef:

zef: Już widzę że pierwsze pole wyszło za duże, z rysunku widać że to jest mniej niż 1j² a mi wyszło √2j² Mógłby ktoś poprawić ?

zef: y=√x ⇒x=y² y=−x+2 ⇒ x=2−y

	y3		y2		1		1
|∫01(y2−2+y)dy|=||		−2y+		|01|=|		−2+		|=
	3		2		3		2

	2		12		3		7
|		−		+		|=		Tutaj już wyszedł w miarę realny wynik, sprawdzi ktoś ?
	6		6		6		6

Pytający: https://www.wolframalpha.com/input/?i=integral+from+0+to+1+of+sqrt(x)+%2B+integral+from+1+to+2+of+-x%2B2

zef: Czyli za pierwszym razem granice wyznaczyłem dobrze, tylko musiałem machnąć się w obliczeniach. Jak pocałkowałem po zmiennej y to wyszło, w tym przypadku po y jest łatwiej

Pytający: Ano tu się machnąłeś:

	2x3/2		2		23/2
|		|01=		≠
	3		3		3

zef: No faktycznie, dziękuję ! Jakby ktoś miał jakieś pole do obliczenia to podsyłać

Jack: Powrót do całek ?

zef: Dopiero po maturze ! Chciałem sobie dzisiaj takie podstawy przypomnieć jedynie, może mi się przyda do geometrii analitycznej

Jack: https://www.wolframalpha.com/input/?i=area+between+functions

zef: Dzięki Jack, przyda się

Metis: zef nie zajmuj siętym czym teraz nie musisz skup się na geometrii i reszcie− progi pójdą do góry, walcz

Metis: O całki na maturze nikt Cię nie zapyta

zef: Pomagam tutaj, ale jakoś żeby się zabrać za przygotowanie do matury to nie ma chęci :<. Jednak chyba będzie trzeba zacząć robić jakieś zadania ze zbiorów.

Alky: Przypadkiem wpadłem na ten temat. Jakbyś jeszcze chciał sobie coś policzyć z tego zakresu materiału to mam kilka przykładów. https://scr.hu/P1BAdl https://scr.hu/RDKoOw I kolejno odpowiedzi, jakbyś chciał sobie sprawdzić. https://scr.hu/AKYlBV https://scr.hu/lngldB

Mariusz: Alky przejrzyj sobie te zadania http://www.cs.put.poznan.pl/aswiercz/zestaw3.htm

Alky: Hmm, nie bawiłem się jeszcze stricte listami jednokierunkowymi, ale w ten weekend jak będę miał czas i siły to się chętnie doedukuje. Fajnie, dzięki